Title here
Summary here
Solving Linear Parabolic Pde Systems With Coupled Ode Systems
This tutorial is automatically generated from TestSolvingLinearParabolicPdeSystemsWithCoupledOdeSystemsTutorial.hpp at revision 8422a2c1f0b1. Note that the code is given in full at the bottom of the page.
Examples showing how to solve a system of coupled linear parabolic PDEs and ODEs
In this tutorial we show how Chaste can be used to solve a system of coupled linear
parabolic PDEs and ODEs. This test uses the LinearParabolicPdeSystemWithCoupledOdeSystemSolver.
The following header files need to be included. First we include the header needed to define this class as a test suite.
#include <cxxtest/TestSuite.h>On some systems there is a clash between Boost Ublas includes and PETSc. This can be resolved by making sure that Chaste’s interface to the Boost libraries are included as early as possible.
#include "UblasIncludes.hpp"This is the class that is needed to solve a system of coupled linear parabolic PDEs and ODEs.
#include "LinearParabolicPdeSystemWithCoupledOdeSystemSolver.hpp"The next header file defines the Schnackenberg system, which comprises two reaction-diffusion PDEs that are coupled through their reaction terms.
#include "SchnackenbergCoupledPdeSystem.hpp"The next header file will allow us to specify a random initial condition.
#include "RandomNumberGenerator.hpp"We then include header files that allow us to specify boundary conditions for the PDEs,
deal with meshes and output files, and use PETSc. As noted before, PetscSetupAndFinalize.hpp
must be included in every test that uses PETSc.
#include "BoundaryConditionsContainer.hpp"
#include "ConstBoundaryCondition.hpp"
#include "OutputFileHandler.hpp"
#include "TrianglesMeshReader.hpp"
#include "PetscSetupAndFinalize.hpp"Test 1: Solving the Schnackenberg system
Here, we solve the Schnackenberg system of PDEs, given by
$$ \begin{align*} u_t &= \nabla. (D_1 \nabla u) + k_1 - k_{-1}u + k_3 u^2 v,\\\ v_t &= \nabla. (D_2 \nabla v) + k_2 -k_3 u^2 v, \end{align*} $$
on a 2d butterfly-shaped domain. We impose non-zero Dirichlet boundary conditions and an initial condition that is a random perturbation of the spatially uniform steady state of the system.
To do this we define the test suite (a class). It is sensible to name it the same
as the filename. The class should inherit from CxxTest::TestSuite.
class TestSolvingLinearParabolicPdeSystemsWithCoupledOdeSystemsTutorial : public CxxTest::TestSuite
{All individual tests defined in this test suite must be declared as public.
public:Define a particular test.
void TestSchnackenbergSystemOnButterflyMesh()
{As usual, we first create a mesh. Here we are using a 2d mesh of a butterfly-shaped domain.
TrianglesMeshReader<2,2> mesh_reader("mesh/test/data/butterfly");
TetrahedralMesh<2,2> mesh;
mesh.ConstructFromMeshReader(mesh_reader);We scale the mesh to an appropriate size.
mesh.Scale(0.2, 0.2);Next, we instantiate the PDE system to be solved. We pass the parameter values into the constructor. (The order is $D_1, D_2, k_1, k_{-1}, k_2, k_3$)
SchnackenbergCoupledPdeSystem<2> pde(1e-4, 1e-2, 0.1, 0.2, 0.3, 0.1);Then we have to define the boundary conditions. As we are in 2d, SPACE_DIM=2 and
ELEMENT_DIM=2. We also have two unknowns u and v,
so in this case PROBLEM_DIM=2. The value of each boundary condition is
given by the spatially uniform steady state solution of the Schnackenberg system,
given by $u = (k_1 + k_2)/k_{-1}$, $v = k_2 k_{-1}^2 / k_3(k_1 + k_2)^2$.
BoundaryConditionsContainer<2,2,2> bcc;
ConstBoundaryCondition<2>* p_bc_for_u = new ConstBoundaryCondition<2>(2.0);
ConstBoundaryCondition<2>* p_bc_for_v = new ConstBoundaryCondition<2>(0.75);
for (TetrahedralMesh<2,2>::BoundaryNodeIterator node_iter = mesh.GetBoundaryNodeIteratorBegin();
node_iter != mesh.GetBoundaryNodeIteratorEnd();
++node_iter)
{
bcc.AddDirichletBoundaryCondition(*node_iter, p_bc_for_u, 0);
bcc.AddDirichletBoundaryCondition(*node_iter, p_bc_for_v, 1);
}This is the solver for solving coupled systems of linear parabolic PDEs and ODEs, which takes in the mesh, the PDE system, the boundary conditions and optionally a vector of ODE systems (one for each node in the mesh). Since in this example we are solving a system of coupled PDEs only, we do not supply this last argument.
LinearParabolicPdeSystemWithCoupledOdeSystemSolver<2,2,2> solver(&mesh, &pde, &bcc);Then we set the end time and time step and the output directory to which results will be written.
double t_end = 10;
solver.SetTimes(0, t_end);
solver.SetTimeStep(1e-1);
solver.SetSamplingTimeStep(1);
solver.SetOutputDirectory("TestSchnackenbergSystemOnButterflyMesh");We create a vector of initial conditions for u and v that are random perturbations of the spatially uniform steady state and pass this to the solver.
std::vector<double> init_conds(2*mesh.GetNumNodes());
for (unsigned i=0; i<mesh.GetNumNodes(); i++)
{
init_conds[2*i] = fabs(2.0 + RandomNumberGenerator::Instance()->ranf());
init_conds[2*i + 1] = fabs(0.75 + RandomNumberGenerator::Instance()->ranf());
}
Vec initial_condition = PetscTools::CreateVec(init_conds);
solver.SetInitialCondition(initial_condition);We now solve the PDE system and write results to VTK files, for
visualization using Paraview. Results will be written to $CHASTE_TEST_OUTPUT/TestSchnackenbergSystemOnButterflyMesh
as a results.pvd file and several results_[time].vtu files.
You should see something like 
for
u and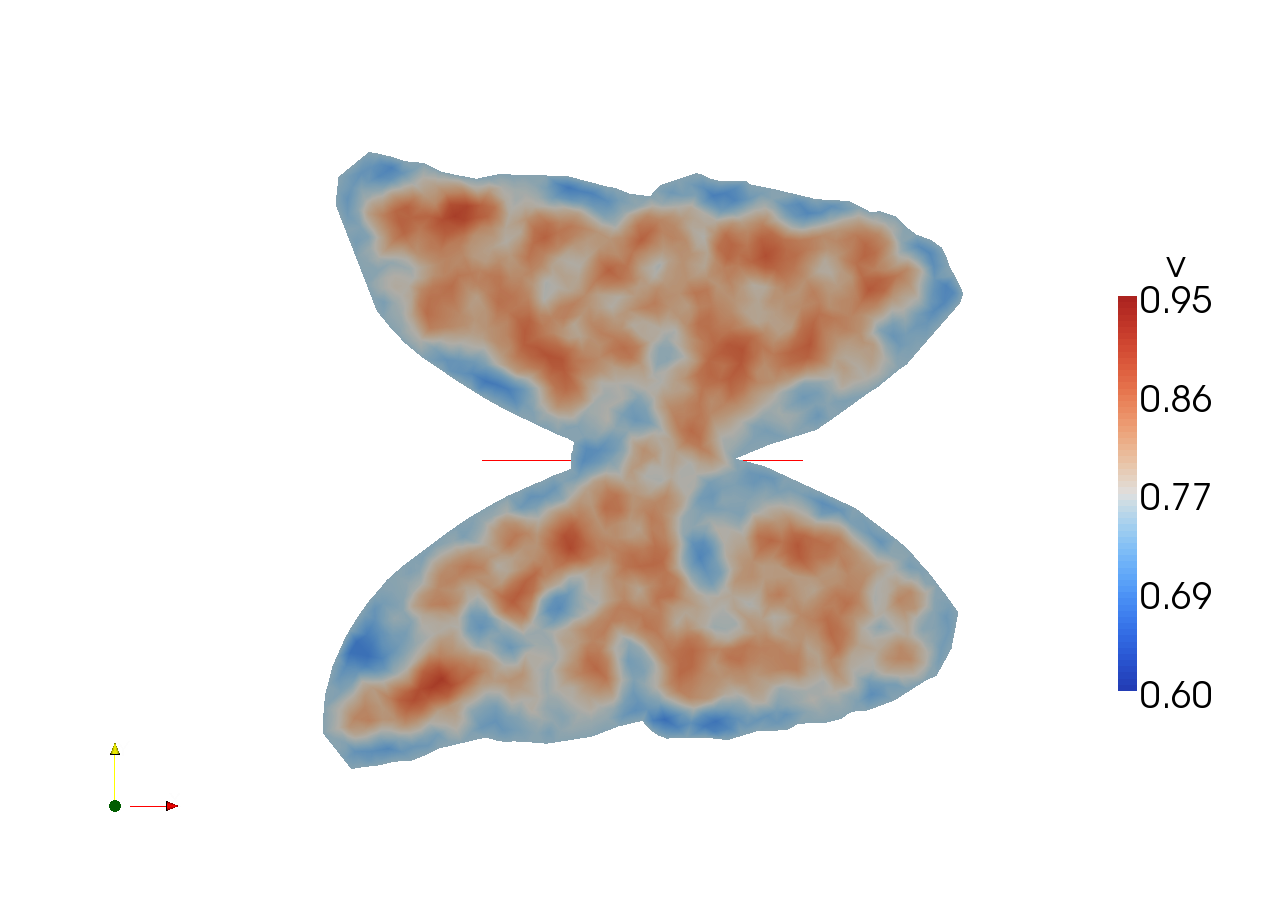 
for v.
solver.SolveAndWriteResultsToFile();All PETSc Vecs should be destroyed when they are no longer needed.
PetscTools::Destroy(initial_condition);
}
};Full code
#include <cxxtest/TestSuite.h>
#include "UblasIncludes.hpp"
#include "LinearParabolicPdeSystemWithCoupledOdeSystemSolver.hpp"
#include "SchnackenbergCoupledPdeSystem.hpp"
#include "RandomNumberGenerator.hpp"
#include "BoundaryConditionsContainer.hpp"
#include "ConstBoundaryCondition.hpp"
#include "OutputFileHandler.hpp"
#include "TrianglesMeshReader.hpp"
#include "PetscSetupAndFinalize.hpp"
class TestSolvingLinearParabolicPdeSystemsWithCoupledOdeSystemsTutorial : public CxxTest::TestSuite
{
public:
void TestSchnackenbergSystemOnButterflyMesh()
{
TrianglesMeshReader<2,2> mesh_reader("mesh/test/data/butterfly");
TetrahedralMesh<2,2> mesh;
mesh.ConstructFromMeshReader(mesh_reader);
mesh.Scale(0.2, 0.2);
SchnackenbergCoupledPdeSystem<2> pde(1e-4, 1e-2, 0.1, 0.2, 0.3, 0.1);
BoundaryConditionsContainer<2,2,2> bcc;
ConstBoundaryCondition<2>* p_bc_for_u = new ConstBoundaryCondition<2>(2.0);
ConstBoundaryCondition<2>* p_bc_for_v = new ConstBoundaryCondition<2>(0.75);
for (TetrahedralMesh<2,2>::BoundaryNodeIterator node_iter = mesh.GetBoundaryNodeIteratorBegin();
node_iter != mesh.GetBoundaryNodeIteratorEnd();
++node_iter)
{
bcc.AddDirichletBoundaryCondition(*node_iter, p_bc_for_u, 0);
bcc.AddDirichletBoundaryCondition(*node_iter, p_bc_for_v, 1);
}
LinearParabolicPdeSystemWithCoupledOdeSystemSolver<2,2,2> solver(&mesh, &pde, &bcc);
double t_end = 10;
solver.SetTimes(0, t_end);
solver.SetTimeStep(1e-1);
solver.SetSamplingTimeStep(1);
solver.SetOutputDirectory("TestSchnackenbergSystemOnButterflyMesh");
std::vector<double> init_conds(2*mesh.GetNumNodes());
for (unsigned i=0; i<mesh.GetNumNodes(); i++)
{
init_conds[2*i] = fabs(2.0 + RandomNumberGenerator::Instance()->ranf());
init_conds[2*i + 1] = fabs(0.75 + RandomNumberGenerator::Instance()->ranf());
}
Vec initial_condition = PetscTools::CreateVec(init_conds);
solver.SetInitialCondition(initial_condition);
solver.SolveAndWriteResultsToFile();
PetscTools::Destroy(initial_condition);
}
};