Title here
Summary here
Documentation for Release 2024.1
Element Local Index Numbering Convention
Linear elements
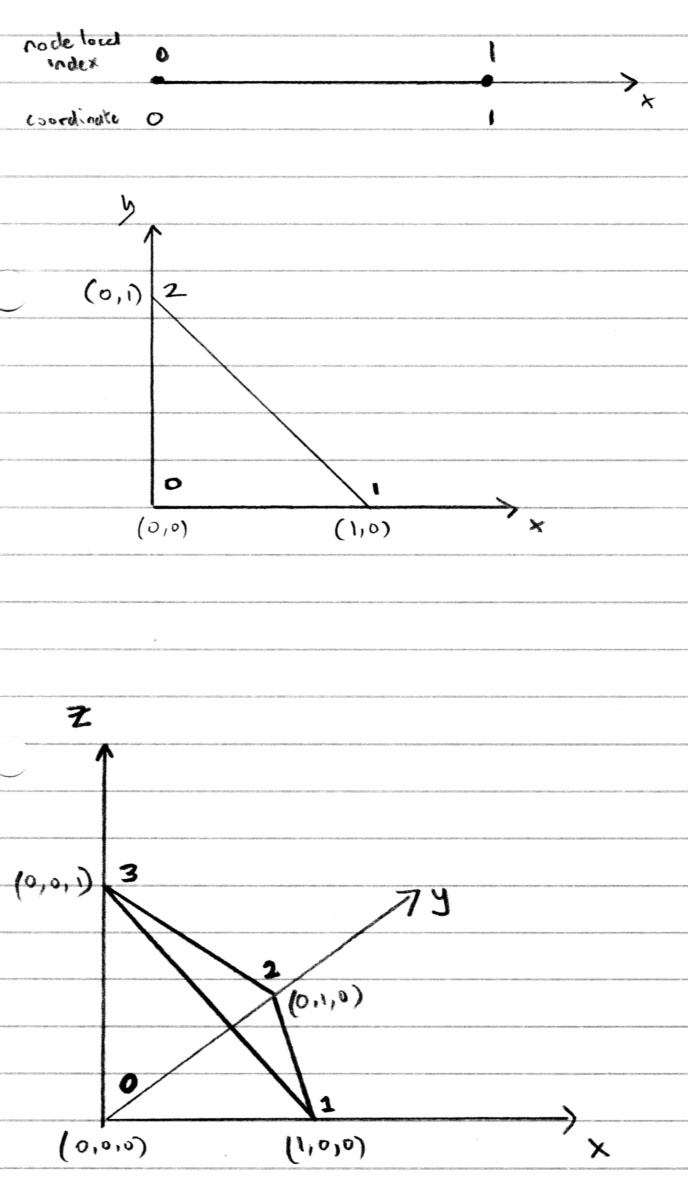
See image below for the local numbering of 1D, 2D, and 3D simplices (tetrahedral elements).
Numbering for a line is clear, left to right.
Numbering for the triangles has to be done in anticlockwise fashion, important for the Jacobian matrices (to have positive determinant).
Numbering for the tetrahedrons has to be done using the right hand rule1, important for the Jacobian matrices (to have positive determinant).
Quadratic elements
Triangles
- Vertices are nodes 0, 1, 2.
- Node 4 is opposite node 0.
- Node 5 is opposite node 1.
- Node 6 is opposite node 2.
Tetrahedra
- Vertices are nodes 0,1,2,3.
- The following table gives the two vertices adjacent to each internal node:
| Internal node | Adjacent vertices |
|---|---|
| 4 | 0, 1 |
| 5 | 1, 2 |
| 6 | 0, 2 |
| 7 | 0, 3 |
| 8 | 1, 3 |
| 9 | 2, 3 |
These are the same as Triangle or TetGen.
Right hand rule: form three orthognal axis with the thumb, index and middle finger, then the first node is junction of thumb and index, second node is the end of the thumb, third node is the end of the index, fourth node is at the end of the middle finger. (ever done some cross-products?) ↩︎