AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > Class Template Reference

#include <AbstractAssembler.hpp>

Inheritance diagram for AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >:

Collaboration diagram for AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >:

List of all members.

Public Member Functions

AbstractAssembler ()

void SetBoundaryConditionsContainer (BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > *pBoundaryConditions)

virtual ~AbstractAssembler ()

virtual void ResetInterpolatedQuantities (void)

virtual void IncrementInterpolatedQuantities (double phi_i, const Node< SPACE_DIM > *pNode)

Protected Member Functions

virtual void SetMatrixIsConst (bool matrixIsConstant=true)

virtual c_matrix< double,
PROBLEM_DIM *(ELEMENT_DIM+1),
PROBLEM_DIM *(ELEMENT_DIM+1)> ComputeMatrixTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, ELEMENT_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, PROBLEM_DIM > &u, c_matrix< double, PROBLEM_DIM, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement)=0

virtual c_vector< double,
PROBLEM_DIM *(ELEMENT_DIM+1)> ComputeVectorTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, ELEMENT_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, PROBLEM_DIM > &u, c_matrix< double, PROBLEM_DIM, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement)=0

virtual c_vector< double,
PROBLEM_DIM *ELEMENT_DIM > ComputeVectorSurfaceTerm (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, ELEMENT_DIM > &rPhi, ChastePoint< SPACE_DIM > &rX)=0

virtual void AssembleOnElement (Element< ELEMENT_DIM, SPACE_DIM > &rElement, c_matrix< double, PROBLEM_DIM *(ELEMENT_DIM+1), PROBLEM_DIM *(ELEMENT_DIM+1) > &rAElem, c_vector< double, PROBLEM_DIM *(ELEMENT_DIM+1)> &rBElem, bool assembleVector, bool assembleMatrix)=0

virtual void AssembleOnSurfaceElement (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, PROBLEM_DIM *ELEMENT_DIM > &rBSurfElem)=0

virtual void AssembleSystem (bool assembleVector, bool assembleMatrix, Vec currentSolutionOrGuess=NULL, double currentTime=0.0)=0

virtual void PrepareForSolve ()=0

virtual void PrepareForAssembleSystem (Vec currentSolutionOrGuess, double currentTime)

virtual void FinaliseAssembleSystem (Vec currentSolutionOrGuess, double currentTime)

virtual void FinaliseLinearSystem (Vec currentSolutionOrGuess, double currentTime, bool assembleVector, bool assembleMatrix)

virtual void ApplyDirichletConditions (Vec currentSolutionOrGuess, bool applyToMatrix)=0

virtual bool ProblemIsNonlinear ()=0

virtual Vec StaticSolve (Vec currentSolutionOrGuess=NULL, double currentTime=0.0, bool assembleMatrix=true)=0

virtual void InitialiseForSolve (Vec initialGuess)=0

virtual LinearSystem ** GetLinearSystem ()=0

virtual ReplicatableVector & rGetCurrentSolutionOrGuess ()=0

void ApplyNeummanBoundaryConditions ()

Protected Attributes

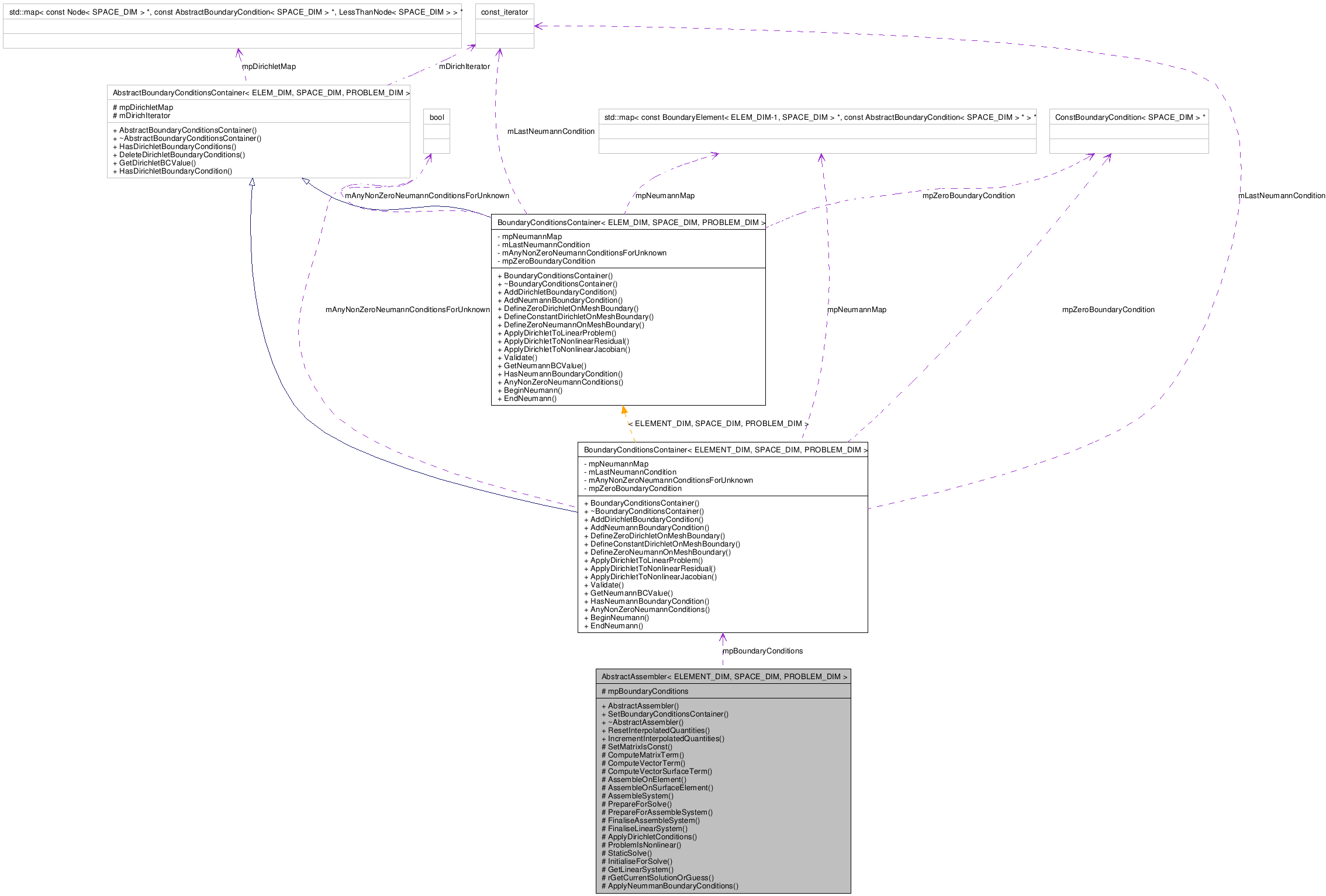
BoundaryConditionsContainer
< ELEMENT_DIM, SPACE_DIM,
PROBLEM_DIM > * mpBoundaryConditions

Detailed Description

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>
class AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >

AbstractAssembler

Base class from which all solvers for linear and nonlinear PDEs inherit. Templated over the PROBLEM_DIM so also handles problems with more than one unknown variable (ie those of the form u_xx + v = 0, v_xx + 2u = 1, where PROBLEM_DIM is equal to 2)

It defines a common interface for AssembleSystem, AssembleOnElement and AssembleOnSurfaceElement. Each of these work for any PROBLEM_DIM>=1. Each of these methods work in both the dynamic case (when there is a current solution available) and the static case. The same code is used for the nonlinear and linear cases. Default code is defined in AbstractStaticAssembler

user calls:

Solve(). In the linear case Solve() calls AssembleSystem() directly, in the nonlinear case Solve() calls the PETSc nonlinear solver which then calls AssembleResidual or AssembleJacobian, both of which call AssembleSystem():

AssembleSystem(). (implemented in AbstractStaticAssembler, loops over elements and adds to the linear system or residual vector or jacobian matrix) AssembleSystem() calls:

AssembleOnElement() and AssembleOnSurfaceElement(). (implemented in AbstractStaticAssembler. These loop over gauss points and create the element stiffness matrix and vector in the linear case ). They call:

ComputeMatrixTerm(), ComputeVectorTerm(), ComputeVectorSurfaceTerm() (implemented in the concrete assembler class (eg SimpleDg0ParabolicAssembler), which tells this assembler exactly what function of bases, position, pde constants etc to add to the element stiffness matrix/vector).

Definition at line 77 of file AbstractAssembler.hpp.

Constructor & Destructor Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AbstractAssembler ( ) [inline]

Default constructor.

Definition at line 330 of file AbstractAssembler.hpp.

References AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpBoundaryConditions.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::~AbstractAssembler ( ) [inline, virtual]

Delete any memory allocated by this class.

Definition at line 348 of file AbstractAssembler.hpp.

Member Function Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::SetMatrixIsConst ( bool matrixIsConstant = true ) [inline, protected, virtual]

Hack for dynamic mixin

Definition at line 86 of file AbstractAssembler.hpp.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual c_matrix<double,PROBLEM_DIM(ELEMENT_DIM+1),PROBLEM_DIM(ELEMENT_DIM+1)> AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ComputeMatrixTerm	(	c_vector< double, ELEMENT_DIM+1 > &	rPhi,
		c_matrix< double, ELEMENT_DIM, ELEMENT_DIM+1 > &	rGradPhi,
		ChastePoint< SPACE_DIM > &	rX,
		c_vector< double, PROBLEM_DIM > &	u,
		c_matrix< double, PROBLEM_DIM, SPACE_DIM > &	rGradU,
		Element< ELEMENT_DIM, SPACE_DIM > *	pElement
	)			`[protected, pure virtual]`

This method returns the matrix to be added to element stiffness matrix for a given gauss point. The arguments are the bases, bases gradients, x and current solution computed at the Gauss point. The returned matrix will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).

--This method has to be implemented in the concrete class--

NOTE: for linear problems rGradU is NOT set up correctly because it should not be needed

Parameters:

	rPhi	The basis functions, rPhi(i) = phi_i, i=1..numBases
	rGradPhi	Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i)
	rX	The point in space
	u	The unknown as a vector, u(i) = u_i
	rGradU	The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j)

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleOnElement().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual c_vector<double,PROBLEM_DIM*(ELEMENT_DIM+1)> AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ComputeVectorTerm	(	c_vector< double, ELEMENT_DIM+1 > &	rPhi,
		c_matrix< double, ELEMENT_DIM, ELEMENT_DIM+1 > &	rGradPhi,
		ChastePoint< SPACE_DIM > &	rX,
		c_vector< double, PROBLEM_DIM > &	u,
		c_matrix< double, PROBLEM_DIM, SPACE_DIM > &	rGradU,
		Element< ELEMENT_DIM, SPACE_DIM > *	pElement
	)			`[protected, pure virtual]`

This method returns the vector to be added to element stiffness vector for a given gauss point. The arguments are the bases, x and current solution computed at the Gauss point. The returned vector will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).

--This method has to be implemented in the concrete class--

NOTE: for linear problems rGradPhi and rGradU are NOT set up correctly because they should not be needed

Parameters:

	rPhi	The basis functions, rPhi(i) = phi_i, i=1..numBases
	rGradPhi	Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i)
	rX	The point in space
	u	The unknown as a vector, u(i) = u_i
	rGradU	The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j)

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleOnElement().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual c_vector<double, PROBLEM_DIM*ELEMENT_DIM> AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ComputeVectorSurfaceTerm	(	const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &	rSurfaceElement,
		c_vector< double, ELEMENT_DIM > &	rPhi,
		ChastePoint< SPACE_DIM > &	rX
	)			`[protected, pure virtual]`

This method returns the vector to be added to element stiffness vector for a given gauss point in BoundaryElement. The arguments are the bases, x and current solution computed at the Gauss point. The returned vector will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).

--This method has to be implemented in the concrete class--

Parameters:

	rSurfaceElement	the element which is being considered.
	rPhi	The basis functions, rPhi(i) = phi_i, i=1..numBases
	rX	The point in space

Implemented in BidomainDg0Assembler< ELEMENT_DIM, SPACE_DIM >, SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >, and BidomainDg0Assembler< DIM, DIM >.

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleOnSurfaceElement().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AssembleOnElement	(	Element< ELEMENT_DIM, SPACE_DIM > &	rElement,
		c_matrix< double, PROBLEM_DIM (ELEMENT_DIM+1), PROBLEM_DIM (ELEMENT_DIM+1) > &	rAElem,
		c_vector< double, PROBLEM_DIM *(ELEMENT_DIM+1)> &	rBElem,
		bool	assembleVector,
		bool	assembleMatrix
	)			`[protected, pure virtual]`

Calculate the contribution of a single element to the linear system.

Parameters:

	rElement	The element to assemble on.
	rAElem	The element's contribution to the LHS matrix is returned in this n by n matrix, where n is the no. of nodes in this element. There is no need to zero this matrix before calling.
	rBElem	The element's contribution to the RHS vector is returned in this vector of length n, the no. of nodes in this element. There is no need to zero this vector before calling.
	currentSolutionOrGuess	For the parabolic linear case, the solution at the current timestep. NULL for the static linear case. In the nonlinear case, the current guess.
	assembleVector	a bool stating whether to assemble the load vector (in the linear case) or the residual vector (in the nonlinear case)
	assembleMatrix	a bool stating whether to assemble the stiffness matrix (in the linear case) or the Jacobian matrix (in the nonlinear case)

Called by AssembleSystem() Calls ComputeMatrixTerm() etc

Implemented in AbstractStaticAssembler

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AssembleOnSurfaceElement	(	const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &	rSurfaceElement,
		c_vector< double, PROBLEM_DIM *ELEMENT_DIM > &	rBSurfElem
	)			`[protected, pure virtual]`

Calculate the contribution of a single surface element with Neumann boundary condition to the linear system.

Parameters:

	rSurfaceElement	The element to assemble on.
	rBSurfElem	The element's contribution to the RHS vector is returned in this vector of length n, the no. of nodes in this element. There is no need to zero this vector before calling.

Implemented in AbstractStaticAssembler

Referenced by AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ApplyNeummanBoundaryConditions().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::PrepareForSolve ( ) [protected, pure virtual]

This method is called at the beginning of Solve(). Subclass assemblers can use it to check everything has been set up correctly

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::PrepareForAssembleSystem	(	Vec	currentSolutionOrGuess,
		double	currentTime
	)			`[inline, protected, virtual]`

This method is called at the beginning of AssembleSystem() and should be overloaded in the concrete assembler class if there is any work to be done before assembling, for example integrating ODEs such as in the Monodomain assembler.

Reimplemented in BidomainDg0Assembler< ELEMENT_DIM, SPACE_DIM >, MonodomainDg0Assembler< ELEMENT_DIM, SPACE_DIM >, and BidomainDg0Assembler< DIM, DIM >.

Definition at line 231 of file AbstractAssembler.hpp.

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleSystem().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::FinaliseAssembleSystem	(	Vec	currentSolutionOrGuess,
		double	currentTime
	)			`[inline, protected, virtual]`

This method is called at the end of AssembleSystem() and should be overloaded in the concrete assembler class if there is any further work to be done

Reimplemented in BidomainDg0Assembler< ELEMENT_DIM, SPACE_DIM >, and BidomainDg0Assembler< DIM, DIM >.

Definition at line 238 of file AbstractAssembler.hpp.

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleSystem().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::FinaliseLinearSystem	(	Vec	currentSolutionOrGuess,
		double	currentTime,
		bool	assembleVector,
		bool	assembleMatrix
	)			`[inline, protected, virtual]`

Can be overloaded if the user needs to edit the linear system after the boundary conditions have been added by before it is solved

Definition at line 245 of file AbstractAssembler.hpp.

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleSystem().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ApplyDirichletConditions	(	Vec	currentSolutionOrGuess,
		bool	applyToMatrix
	)			`[protected, pure virtual]`

This method is called by AssembleSystem to apply dirichlet conditions to the system.

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleSystem().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual bool AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ProblemIsNonlinear ( ) [protected, pure virtual]

Whether grad_u should be calculated

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleOnElement().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual Vec AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::StaticSolve	(	Vec	currentSolutionOrGuess = `NULL`,
		double	currentTime = `0.0`,
		bool	assembleMatrix = `true`
	)			`[protected, pure virtual]`

Perform the work of a single solve, but without any initialisation. Static assemblers must implement this method.

Parameters:

	currentSolutionOrGuess	either the current solution (dynamic problem) or initial guess (static problem); optional in some cases
	currentTime	for a dynamic problem, the current time
	assembleMatrix	whether to assemble the matrix (it may have been done by a previous call)

Returns:: the solution vector

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::InitialiseForSolve ( Vec initialGuess ) [protected, pure virtual]

Perform any initialisation needed before a sequence of StaticSolve calls.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual LinearSystem** AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::GetLinearSystem ( ) [protected, pure virtual]

Accessor methods that subclasses can use to get to useful data.

Referenced by AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ApplyNeummanBoundaryConditions().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ApplyNeummanBoundaryConditions ( ) [inline, protected]

Apply Neumann boundary conditions to the RHS vector by looping over surface elements (though actually looping over the boundary condition objects).

Note for PROBLEM_DIM>1. We assume that if an element has a boundary condition on any unknown there is a boundary condition on unknown 0. This can be so for any problem by adding zero constant conditions where required although this is a bit inefficient. Proper solution involves changing BCC to have a map of arrays boundary conditions rather than an array of maps.

Definition at line 299 of file AbstractAssembler.hpp.

References BoundaryConditionsContainer< ELEM_DIM, SPACE_DIM, PROBLEM_DIM >::AnyNonZeroNeumannConditions(), AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AssembleOnSurfaceElement(), GenericEventHandler< 11, HeartEventHandler >::BeginEvent(), BoundaryConditionsContainer< ELEM_DIM, SPACE_DIM, PROBLEM_DIM >::BeginNeumann(), GenericEventHandler< 11, HeartEventHandler >::EndEvent(), BoundaryConditionsContainer< ELEM_DIM, SPACE_DIM, PROBLEM_DIM >::EndNeumann(), AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::GetLinearSystem(), and AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpBoundaryConditions.

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleSystem().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::SetBoundaryConditionsContainer ( BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > * pBoundaryConditions ) [inline]

Set the boundary conditions.

Definition at line 339 of file AbstractAssembler.hpp.

References AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpBoundaryConditions.

Referenced by BidomainProblem< DIM >::OnEndOfTimestep(), and SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::SimpleNonlinearEllipticAssembler().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ResetInterpolatedQuantities ( void ) [inline, virtual]

The concrete subclass can overload this and IncrementInterpolatedQuantities() if there are some quantities which need to be computed at each Gauss point. They are called in AssembleOnElement()

Reimplemented in BidomainDg0Assembler< ELEMENT_DIM, SPACE_DIM >, MonodomainDg0Assembler< ELEMENT_DIM, SPACE_DIM >, and BidomainDg0Assembler< DIM, DIM >.

Definition at line 361 of file AbstractAssembler.hpp.

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleOnElement(), and AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleOnSurfaceElement().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

virtual void AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::IncrementInterpolatedQuantities	(	double	phi_i,
		const Node< SPACE_DIM > *	pNode
	)			`[inline, virtual]`

The concrete subclass can overload this and ResetInterpolatedQuantities() if there are some quantities which need to be computed at each Gauss point. They are called in AssembleOnElement()

Reimplemented in BidomainDg0Assembler< ELEMENT_DIM, SPACE_DIM >, MonodomainDg0Assembler< ELEMENT_DIM, SPACE_DIM >, and BidomainDg0Assembler< DIM, DIM >.

Definition at line 369 of file AbstractAssembler.hpp.

Referenced by AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleOnElement(), and AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, NON_HEART, MonodomainRhsMatrixAssembler< DIM > >::AssembleOnSurfaceElement().

Member Data Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>

BoundaryConditionsContainer<ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM>* AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpBoundaryConditions [protected]

Boundary conditions to be applied

Definition at line 82 of file AbstractAssembler.hpp.

The documentation for this class was generated from the following file:

/tmp/release_1/pde/src/solver/common/AbstractAssembler.hpp


Public Member Functions
	AbstractAssembler ()
void	SetBoundaryConditionsContainer (BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > *pBoundaryConditions)
virtual	~AbstractAssembler ()
virtual void	ResetInterpolatedQuantities (void)
virtual void	IncrementInterpolatedQuantities (double phi_i, const Node< SPACE_DIM > *pNode)
Protected Member Functions
virtual void	SetMatrixIsConst (bool matrixIsConstant=true)
virtual c_matrix< double, PROBLEM_DIM (ELEMENT_DIM+1), PROBLEM_DIM (ELEMENT_DIM+1)>	ComputeMatrixTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, ELEMENT_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, PROBLEM_DIM > &u, c_matrix< double, PROBLEM_DIM, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement)=0
virtual c_vector< double, PROBLEM_DIM *(ELEMENT_DIM+1)>	ComputeVectorTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, ELEMENT_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, PROBLEM_DIM > &u, c_matrix< double, PROBLEM_DIM, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement)=0
virtual c_vector< double, PROBLEM_DIM *ELEMENT_DIM >	ComputeVectorSurfaceTerm (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, ELEMENT_DIM > &rPhi, ChastePoint< SPACE_DIM > &rX)=0
virtual void	AssembleOnElement (Element< ELEMENT_DIM, SPACE_DIM > &rElement, c_matrix< double, PROBLEM_DIM (ELEMENT_DIM+1), PROBLEM_DIM (ELEMENT_DIM+1) > &rAElem, c_vector< double, PROBLEM_DIM *(ELEMENT_DIM+1)> &rBElem, bool assembleVector, bool assembleMatrix)=0
virtual void	AssembleOnSurfaceElement (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, PROBLEM_DIM *ELEMENT_DIM > &rBSurfElem)=0
virtual void	AssembleSystem (bool assembleVector, bool assembleMatrix, Vec currentSolutionOrGuess=NULL, double currentTime=0.0)=0
virtual void	PrepareForSolve ()=0
virtual void	PrepareForAssembleSystem (Vec currentSolutionOrGuess, double currentTime)
virtual void	FinaliseAssembleSystem (Vec currentSolutionOrGuess, double currentTime)
virtual void	FinaliseLinearSystem (Vec currentSolutionOrGuess, double currentTime, bool assembleVector, bool assembleMatrix)
virtual void	ApplyDirichletConditions (Vec currentSolutionOrGuess, bool applyToMatrix)=0
virtual bool	ProblemIsNonlinear ()=0
virtual Vec	StaticSolve (Vec currentSolutionOrGuess=NULL, double currentTime=0.0, bool assembleMatrix=true)=0
virtual void	InitialiseForSolve (Vec initialGuess)=0
virtual LinearSystem **	GetLinearSystem ()=0
virtual ReplicatableVector &	rGetCurrentSolutionOrGuess ()=0
void	ApplyNeummanBoundaryConditions ()
Protected Attributes
BoundaryConditionsContainer < ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > *	mpBoundaryConditions

AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > Class Template Reference

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM> class AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>
class AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >