AbstractMaterialLaw< DIM > Class Template Reference

#include <AbstractMaterialLaw.hpp>

Inheritance diagram for AbstractMaterialLaw< DIM >:

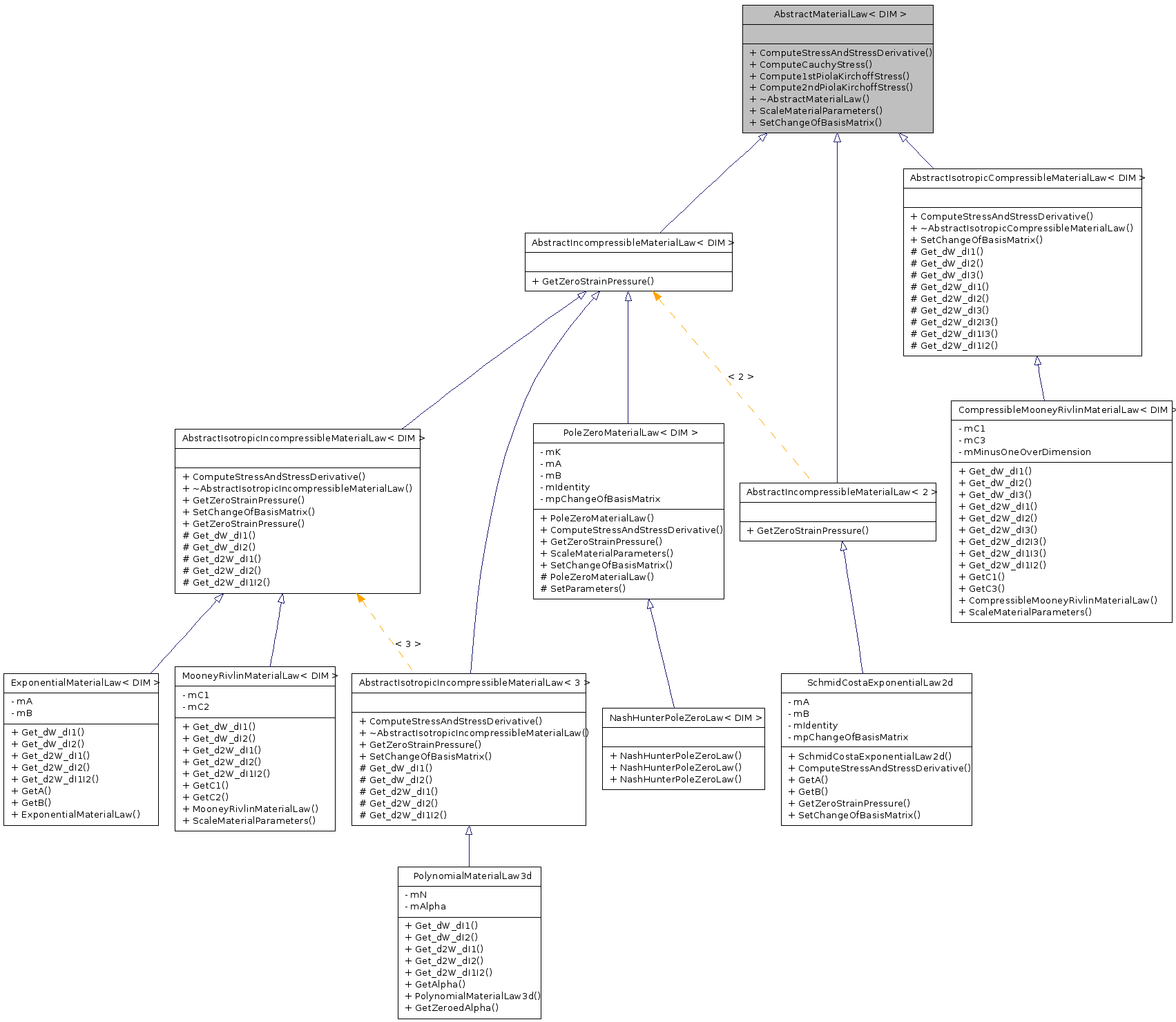
Inheritance graph
[legend]

List of all members.

Public Member Functions

virtual void ComputeStressAndStressDerivative (c_matrix< double, DIM, DIM > &rC, c_matrix< double, DIM, DIM > &rInvC, double pressure, c_matrix< double, DIM, DIM > &rT, FourthOrderTensor< DIM, DIM, DIM, DIM > &rDTdE, bool computeDTdE)=0
void ComputeCauchyStress (c_matrix< double, DIM, DIM > &rF, double pressure, c_matrix< double, DIM, DIM > &rSigma)
void Compute1stPiolaKirchoffStress (c_matrix< double, DIM, DIM > &rF, double pressure, c_matrix< double, DIM, DIM > &rS)
void Compute2ndPiolaKirchoffStress (c_matrix< double, DIM, DIM > &rC, double pressure, c_matrix< double, DIM, DIM > &rT)
virtual ~AbstractMaterialLaw ()
virtual void ScaleMaterialParameters (double scaleFactor)
virtual void SetChangeOfBasisMatrix (c_matrix< double, DIM, DIM > &rChangeOfBasisMatrix)=0

Detailed Description

template<unsigned DIM>
class AbstractMaterialLaw< DIM >

AbstractMaterialLaw

A hyper-elastic material law for finite elasticity

The law is given by a strain energy function W(E), where E is the strain, such that the stress T = dW/dE

Definition at line 48 of file AbstractMaterialLaw.hpp.

Constructor & Destructor Documentation

template<unsigned DIM>
AbstractMaterialLaw< DIM >::~AbstractMaterialLaw (  )  [inline, virtual]

Destructor.

Definition at line 32 of file AbstractMaterialLaw.cpp.

Member Function Documentation

template<unsigned DIM>
virtual void AbstractMaterialLaw< DIM >::ComputeStressAndStressDerivative ( c_matrix< double, DIM, DIM > &  rC,
c_matrix< double, DIM, DIM > &  rInvC,
double  pressure,
c_matrix< double, DIM, DIM > &  rT,
FourthOrderTensor< DIM, DIM, DIM, DIM > &  rDTdE,
bool  computeDTdE 
) [pure virtual]

Compute the (2nd Piola Kirchoff) stress T and the stress derivative dT/dE for a given strain.

NOTE: the strain E is not expected to be passed in, instead the Lagrangian deformation tensor C is required (recall, E = 0.5(C-I))

dTdE is a fourth-order tensor, where dTdE(M,N,P,Q) = dT^{MN}/dE_{PQ}

Parameters:
rC The Lagrangian deformation tensor (F^T F)
rInvC The inverse of C. Should be computed by the user.
pressure the current pressure
rT the stress will be returned in this parameter
rDTdE the stress derivative will be returned in this parameter, assuming the final parameter is true
computeDTdE a boolean flag saying whether the stress derivative is required or not.

Implemented in AbstractIsotropicCompressibleMaterialLaw< DIM >, AbstractIsotropicIncompressibleMaterialLaw< DIM >, PoleZeroMaterialLaw< DIM >, and AbstractIsotropicIncompressibleMaterialLaw< 3 >.

Referenced by AbstractMaterialLaw< DIM >::Compute1stPiolaKirchoffStress(), AbstractMaterialLaw< DIM >::Compute2ndPiolaKirchoffStress(), AbstractMaterialLaw< DIM >::ComputeCauchyStress(), NonlinearElasticitySolver< DIM >::ComputeStressAndStressDerivative(), CompressibleNonlinearElasticitySolver< DIM >::ComputeStressAndStressDerivative(), and AbstractCardiacMechanicsSolver< DIM >::ComputeStressAndStressDerivative().

template<unsigned DIM>
void AbstractMaterialLaw< DIM >::ComputeCauchyStress ( c_matrix< double, DIM, DIM > &  rF,
double  pressure,
c_matrix< double, DIM, DIM > &  rSigma 
) [inline]

Compute the Cauchy stress (the true stress), given the deformation gradient F and the pressure. The Cauchy stress is given by

sigma^{ij} = (1/detF) F^i_M T^{MN} F^j_N

where T is the 2nd Piola Kirchoff stress, dW/dE

Parameters:
rF the deformation gradient
pressure the pressure
rSigma an empty matrix, which will be filled in with the Cauchy stress
Note: the compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0

Definition at line 37 of file AbstractMaterialLaw.cpp.

References AbstractMaterialLaw< DIM >::ComputeStressAndStressDerivative(), Determinant(), and Inverse().

template<unsigned DIM>
void AbstractMaterialLaw< DIM >::Compute1stPiolaKirchoffStress ( c_matrix< double, DIM, DIM > &  rF,
double  pressure,
c_matrix< double, DIM, DIM > &  rS 
) [inline]

Compute the 1st Piola Kirchoff stress, given the deformation gradient F and the pressure. The 1st Piola Kirchoff stress given by

S^{Mi} = T^{MN} F^i_M,

where T is the 2nd PK stress, dW/dE.

Note that this stress is not symmetric and the least useful of the three stresses.

Parameters:
rF the deformation gradient
pressure the pressure
rS an empty matrix, which will be filled in with the stress
Note: the compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0

Definition at line 73 of file AbstractMaterialLaw.cpp.

References AbstractMaterialLaw< DIM >::ComputeStressAndStressDerivative(), and Inverse().

template<unsigned DIM>
void AbstractMaterialLaw< DIM >::Compute2ndPiolaKirchoffStress ( c_matrix< double, DIM, DIM > &  rC,
double  pressure,
c_matrix< double, DIM, DIM > &  rT 
) [inline]

Compute the 2nd Piola Kirchoff stress, given the deformation tensor C and the pressure. The 2nd Piola Kirchoff stress given by

T^{MN} = dW/dE_{MN} = 2dW/dC_{MN}

Parameters:
rC the Lagrange deformation tensor (C=F^T F), *not* F, and *not* E
pressure the pressure
rT an empty matrix, which will be filled in with the stress
Note: to compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0

Definition at line 90 of file AbstractMaterialLaw.cpp.

References AbstractMaterialLaw< DIM >::ComputeStressAndStressDerivative(), and Inverse().

template<unsigned DIM>
void AbstractMaterialLaw< DIM >::ScaleMaterialParameters ( double  scaleFactor  )  [inline, virtual]

Set a scale factor by which (dimensional) material parameters are scaled. This method can be optionally implemented in the child class; if no implementation is made an exception is thrown. A scale factor may be used/needed to improve GMRES convergence. Note that is a material law is scaled like this any dimensionally equivalent terms (eg gravity, tractions, active tensions) must also be scaled. Also, computed pressure will come out scaled.

Parameters:
scaleFactor the scale factor

Reimplemented in CompressibleMooneyRivlinMaterialLaw< DIM >, MooneyRivlinMaterialLaw< DIM >, and PoleZeroMaterialLaw< DIM >.

Definition at line 102 of file AbstractMaterialLaw.cpp.

References EXCEPTION.

template<unsigned DIM>
virtual void AbstractMaterialLaw< DIM >::SetChangeOfBasisMatrix ( c_matrix< double, DIM, DIM > &  rChangeOfBasisMatrix  )  [pure virtual]

Some material laws (eg pole-zero) may have prefered directions (eg fibre direction), but be implemented to assume the prefered directions are parallel to the X-axis etc. Call this with the change of basis matrix and C will be transformed from the Euclidean coordinate system to the appropriate coordinate system before used to calculate T, which will then be transformed from the appropriate coordinate system back to the Euclidean coordinate system before being returned, as will dTdE

Parameters:
rChangeOfBasisMatrix Change of basis matrix.

Implemented in AbstractIsotropicCompressibleMaterialLaw< DIM >, AbstractIsotropicIncompressibleMaterialLaw< DIM >, PoleZeroMaterialLaw< DIM >, and AbstractIsotropicIncompressibleMaterialLaw< 3 >.

Referenced by AbstractCardiacMechanicsSolver< DIM >::ComputeStressAndStressDerivative().

The documentation for this class was generated from the following files:
Generated on Mon Apr 18 11:36:02 2011 for Chaste by  doxygen 1.5.5