AbstractIncompressibleMaterialLaw< DIM > Class Template Reference

#include <AbstractIncompressibleMaterialLaw.hpp>

Inheritance diagram for AbstractIncompressibleMaterialLaw< DIM >:

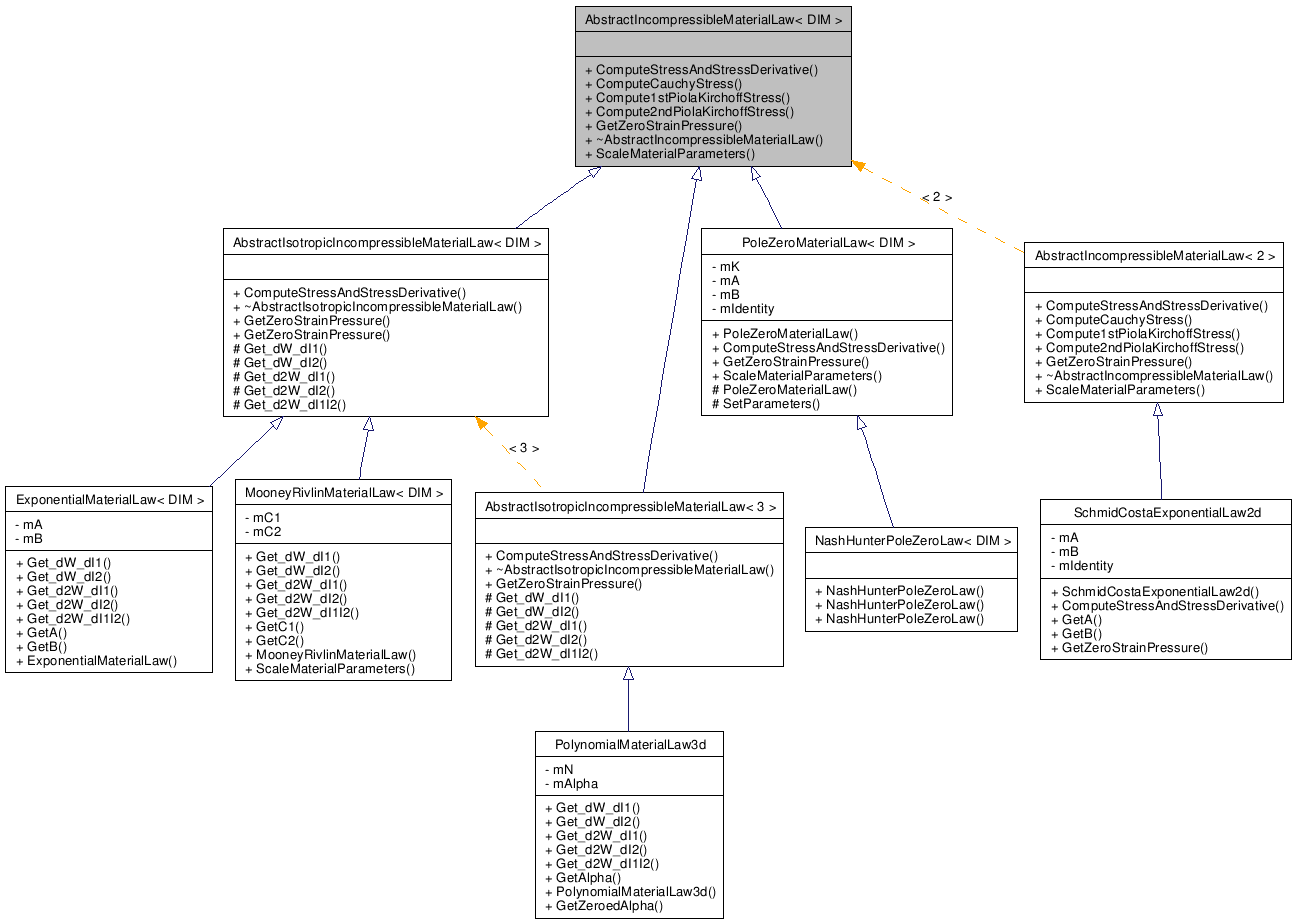
Inheritance graph
[legend]

List of all members.

Public Member Functions

virtual void ComputeStressAndStressDerivative (c_matrix< double, DIM, DIM > &C, c_matrix< double, DIM, DIM > &invC, double pressure, c_matrix< double, DIM, DIM > &T, FourthOrderTensor2< DIM > &dTdE, bool computeDTdE)=0
void ComputeCauchyStress (c_matrix< double, DIM, DIM > &F, double pressure, c_matrix< double, DIM, DIM > &sigma)
void Compute1stPiolaKirchoffStress (c_matrix< double, DIM, DIM > &F, double pressure, c_matrix< double, DIM, DIM > &S)
void Compute2ndPiolaKirchoffStress (c_matrix< double, DIM, DIM > &C, double pressure, c_matrix< double, DIM, DIM > &T)
virtual double GetZeroStrainPressure ()=0
virtual void ScaleMaterialParameters (double scaleFactor)

Detailed Description

template<unsigned DIM>
class AbstractIncompressibleMaterialLaw< DIM >

AbstractIncompressibleMaterialLaw

An incompressible hyperelastic material law for finite elastiticy

The law is given by a strain energy function W(E), where E is the strain, such that the stress T = dW/dE

Definition at line 48 of file AbstractIncompressibleMaterialLaw.hpp.

Member Function Documentation

template<unsigned DIM>
virtual void AbstractIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative ( c_matrix< double, DIM, DIM > &  C,
c_matrix< double, DIM, DIM > &  invC,
double  pressure,
c_matrix< double, DIM, DIM > &  T,
FourthOrderTensor2< DIM > &  dTdE,
bool  computeDTdE 
) [pure virtual]

Compute the (2nd Piola Kirchoff) stress T and the stress derivative dT/dE for a given strain.

NOTE: the strain E is not expected to be passed in, instead the Lagrangian deformation tensor C is required (recall, E = 0.5(C-I))

dT/dE is a fourth-order tensor, where dT/dE[M][N][P][Q] = dT^{MN}/dE_{PQ}

Parameters:
C The Lagrangian deformation tensor (F^T F)
invC The inverse of C. Should be computed by the user. (Change this?)
pressure the current pressure
T the stress will be returned in this parameter
dTdE the stress derivative will be returned in this parameter, assuming the final parameter is true
computeDTdE a boolean flag saying whether the stress derivative is required or not.

Implemented in AbstractIsotropicIncompressibleMaterialLaw< DIM >, PoleZeroMaterialLaw< DIM >, and AbstractIsotropicIncompressibleMaterialLaw< 3 >.

Referenced by NonlinearElasticityAssembler< DIM >::AssembleOnElement(), ImplicitCardiacMechanicsAssembler< DIM >::AssembleOnElement(), AbstractIncompressibleMaterialLaw< DIM >::Compute1stPiolaKirchoffStress(), AbstractIncompressibleMaterialLaw< DIM >::Compute2ndPiolaKirchoffStress(), and AbstractIncompressibleMaterialLaw< DIM >::ComputeCauchyStress().

template<unsigned DIM>
void AbstractIncompressibleMaterialLaw< DIM >::ComputeCauchyStress ( c_matrix< double, DIM, DIM > &  F,
double  pressure,
c_matrix< double, DIM, DIM > &  sigma 
) [inline]

Compute the Cauchy stress (the true stress), given the deformation gradient F and the pressure. The Cauchy stress is given by

sigma^{ij} = (1/detF) F^i_M T^{MN} F^j_N

where T is the 2nd Piola Kirchoff stress, dW/dE

Parameters:
F the deformation gradient
pressure the pressure sigma an empty matrix, which will be filled in with the Cauchy stress
Note: the compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0

Definition at line 37 of file AbstractIncompressibleMaterialLaw.cpp.

References AbstractIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative().

template<unsigned DIM>
void AbstractIncompressibleMaterialLaw< DIM >::Compute1stPiolaKirchoffStress ( c_matrix< double, DIM, DIM > &  F,
double  pressure,
c_matrix< double, DIM, DIM > &  S 
) [inline]

Compute the 1st Piola Kirchoff stress, given the deformation gradient F and the pressure. The 1st Piola Kirchoff stress given by

S^{Mi} = T^{MN} F^i_M,

where T is the 2nd PK stress, dW/dE.

Note that this stress is not symmetric and the least useful of the three stresses.

Parameters:
F the deformation gradient
pressure the pressure S an empty matrix, which will be filled in with the stress
Note: the compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0

Definition at line 71 of file AbstractIncompressibleMaterialLaw.cpp.

References AbstractIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative().

template<unsigned DIM>
void AbstractIncompressibleMaterialLaw< DIM >::Compute2ndPiolaKirchoffStress ( c_matrix< double, DIM, DIM > &  C,
double  pressure,
c_matrix< double, DIM, DIM > &  T 
) [inline]

Compute the 2nd Piola Kirchoff stress, given the deformation tensor C and the pressure. The 2nd Piola Kirchoff stress given by

T^{MN} = dW/dE_{MN} = 2dW/dC_{MN}

Parameters:
C the Lagrange deformation tensor (C=F^T F), *not* F, and *not* E
pressure the pressure T an empty matrix, which will be filled in with the stress
Note: to compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0

Definition at line 86 of file AbstractIncompressibleMaterialLaw.cpp.

References AbstractIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative().

template<unsigned DIM>
virtual double AbstractIncompressibleMaterialLaw< DIM >::GetZeroStrainPressure (  )  [pure virtual]

Get the pressure corresponding to E=0, ie C=identity

Implemented in AbstractIsotropicIncompressibleMaterialLaw< DIM >, PoleZeroMaterialLaw< DIM >, SchmidCostaExponentialLaw2d, AbstractIsotropicIncompressibleMaterialLaw< 3 >, and AbstractIsotropicIncompressibleMaterialLaw< DIM >.

template<unsigned DIM>
void AbstractIncompressibleMaterialLaw< DIM >::ScaleMaterialParameters ( double  scaleFactor  )  [inline, virtual]

Set a scale factor by which (dimensional) material parameters are scaled. This method can be optionally implemented in the child class; if no implementation is made an exception is thrown. A scale factor may be used/needed to improve GMRES convergence. Note that is a material law is scaled like this any dimensionally equivalent terms (eg gravity, tractions, active tensions) must also be scaled. Also, computed pressure will come out scaled.

Reimplemented in MooneyRivlinMaterialLaw< DIM >, and PoleZeroMaterialLaw< DIM >.

Definition at line 96 of file AbstractIncompressibleMaterialLaw.cpp.

The documentation for this class was generated from the following files:
Generated on Wed Mar 18 12:52:05 2009 for Chaste by  doxygen 1.5.5