AbstractIsotropicIncompressibleMaterialLaw< DIM > Class Template Reference

#include <AbstractIsotropicIncompressibleMaterialLaw.hpp>

Inheritance diagram for AbstractIsotropicIncompressibleMaterialLaw< DIM >:

[legend]

Collaboration diagram for AbstractIsotropicIncompressibleMaterialLaw< DIM >:

[legend]

List of all members.

Public Member Functions
void	ComputeStressAndStressDerivative (c_matrix< double, DIM, DIM > &C, c_matrix< double, DIM, DIM > &invC, double pressure, c_matrix< double, DIM, DIM > &T, FourthOrderTensor2< DIM > &dTdE, bool computeDTdE)
double	GetZeroStrainPressure ()
template<>
double	GetZeroStrainPressure ()
Protected Member Functions
virtual double	Get_dW_dI1 (double I1, double I2)=0
virtual double	Get_dW_dI2 (double I1, double I2)=0
virtual double	Get_d2W_dI1 (double I1, double I2)=0
virtual double	Get_d2W_dI2 (double I1, double I2)=0
virtual double	Get_d2W_dI1I2 (double I1, double I2)=0

---

Detailed Description

template<unsigned DIM>
class AbstractIsotropicIncompressibleMaterialLaw< DIM >

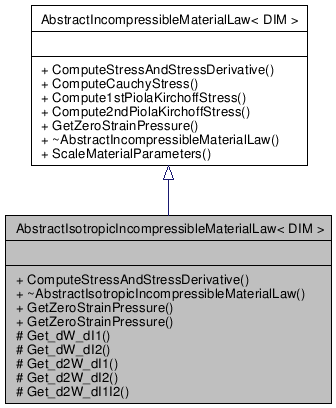
AbstractIsotropicIncompressibleMaterialLaw

An isotropic incompressible hyperelastic material law for finite elastiticy

The law is given by a strain energy function W(I1,I2,I3), where I_i are the principal invariants of C, the Lagrangian deformation tensor. (I1=trace(C), I2=trace(C)^2-trace(C^2), I3=det(C)). Since it is incompressible, the full strain energy has the form W^{full} = W(I_1,I_2) - p/2 C^{-1}

Note: only dimension equals 2 or 3 should be permitted.

Definition at line 48 of file AbstractIsotropicIncompressibleMaterialLaw.hpp.

---

Member Function Documentation

template<unsigned DIM>

void AbstractIsotropicIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative	(	c_matrix< double, DIM, DIM > &	C,
		c_matrix< double, DIM, DIM > &	invC,
		double	pressure,
		c_matrix< double, DIM, DIM > &	T,
		FourthOrderTensor2< DIM > &	dTdE,
		bool	computeDTdE
	)			[inline, virtual]

Compute the (2nd Piola Kirchoff) stress T and the stress derivative dT/dE for a given strain.

NOTE: the strain E is not expected to be passed in, instead the Lagrangian deformation tensor C is required (recall, E = 0.5(C-I)

dT/dE is a fourth-order tensor, where dT/dE(M,N,P,Q) = dT^{MN}/dE_{PQ}

Parameters:

	C	The Lagrangian deformation tensor (F^T F)
	invC	The inverse of C. Should be computed by the user. (Change this?)
	pressure	the current pressure
	T	the stress will be returned in this parameter
	dTdE	the stress derivative will be returned in this parameter, assuming the final parameter is true
	computeDTdE	a boolean flag saying whether the stress derivative is required or not.

This is the implemtation for an isotropic material law, so the stress etc is computed by calling methods returning dW/dI1, dW/dI2 etc.

Implements AbstractIncompressibleMaterialLaw< DIM >.

Definition at line 37 of file AbstractIsotropicIncompressibleMaterialLaw.cpp.

template<unsigned DIM>

double AbstractIsotropicIncompressibleMaterialLaw< DIM >::GetZeroStrainPressure

(

)

[virtual]

Get the pressure corresponding to E=0, ie corresponding to C=identity

Since T = 2*Get_dW_dI1 identity + 4*Get_dW_dI2 (I1*identity - C) - p inverse(C), this is equal to 2*Get_dW_dI1(3,3) + 4*Get_dW_dI2(3,3) in 3D

Implements AbstractIncompressibleMaterialLaw< DIM >.

template<>

double AbstractIsotropicIncompressibleMaterialLaw< 2 >::GetZeroStrainPressure

(

)

[inline, virtual]

Get the pressure corresponding to E=0, ie C=identity

Implements AbstractIncompressibleMaterialLaw< DIM >.

Definition at line 133 of file AbstractIsotropicIncompressibleMaterialLaw.cpp.

---

The documentation for this class was generated from the following files:

• /tmp/release_1/pde/src/problem/common/AbstractIsotropicIncompressibleMaterialLaw.hpp
• /tmp/release_1/pde/src/problem/common/AbstractIsotropicIncompressibleMaterialLaw.cpp