SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM > Class Template Reference

#include <SimpleNonlinearEllipticAssembler.hpp>

Inherits AbstractNonlinearAssembler< ELEMENT_DIM, SPACE_DIM, 1, SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM > >.

Collaboration diagram for SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >:
Collaboration graph
[legend]

List of all members.

Public Types

typedef
SimpleNonlinearEllipticAssembler
< ELEMENT_DIM, SPACE_DIM > 		SelfType
typedef
AbstractNonlinearAssembler
< ELEMENT_DIM, SPACE_DIM,
1, SelfType > 		BaseClassType

Public Member Functions

 SimpleNonlinearEllipticAssembler (AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *pMesh, AbstractNonlinearEllipticPde< SPACE_DIM > *pPde, BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 1 > *pBoundaryConditions, unsigned numQuadPoints=2)

Static Public Attributes

static const unsigned E_DIM = ELEMENT_DIM
static const unsigned S_DIM = SPACE_DIM
static const unsigned P_DIM = 1u

Private Member Functions

virtual c_matrix< double,
1 *(ELEMENT_DIM+1),
1 *(ELEMENT_DIM+1)> 		ComputeMatrixTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, 1 > &rU, c_matrix< double, 1, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement)
virtual c_vector< double,
1 *(ELEMENT_DIM+1)> 		ComputeVectorTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, 1 > &rU, c_matrix< double, 1, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement)
virtual c_vector< double,
1 *ELEMENT_DIM > 		ComputeVectorSurfaceTerm (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, ELEMENT_DIM > &rPhi, ChastePoint< SPACE_DIM > &rX)

Private Attributes

AbstractNonlinearEllipticPde
< SPACE_DIM > * 		mpNonlinearEllipticPde

Friends

class AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, 1, true, SelfType >
class TestSimpleNonlinearEllipticAssembler

Detailed Description

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
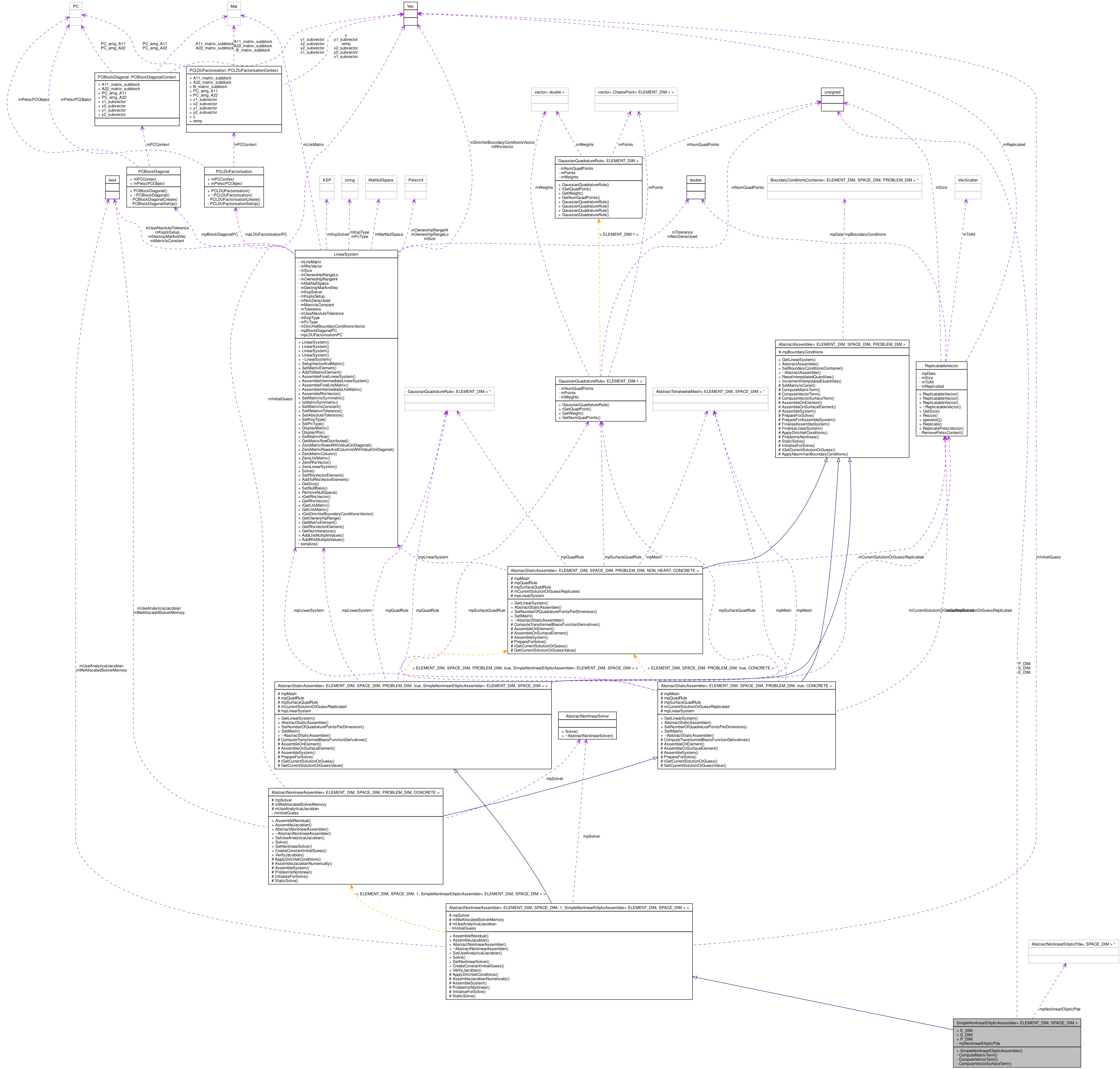
class SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >

Concrete simple class that assembles and solves the nonlinear system for a nonlinear elliptic PDE.

USAGE: call the constructor with the mesh, pde and boundary conditions, then call Solve() with the initial guess.

Todo:
[old todo, maybe not true anymore after refactor(?)] #1298 This class could do with some tidying. More (3D) tests are also needed. It probably needs re-writing to take advantage of parallel machines.

Definition at line 49 of file SimpleNonlinearEllipticAssembler.hpp.

Member Typedef Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
typedef AbstractNonlinearAssembler<ELEMENT_DIM, SPACE_DIM, 1, SelfType> SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::BaseClassType

Base class type (to save typing).

Reimplemented from AbstractNonlinearAssembler< ELEMENT_DIM, SPACE_DIM, 1, SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM > >.

Definition at line 58 of file SimpleNonlinearEllipticAssembler.hpp.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
typedef SimpleNonlinearEllipticAssembler<ELEMENT_DIM, SPACE_DIM> SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::SelfType

This type (to save typing).

Definition at line 57 of file SimpleNonlinearEllipticAssembler.hpp.

Constructor & Destructor Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::SimpleNonlinearEllipticAssembler ( AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *  pMesh,
AbstractNonlinearEllipticPde< SPACE_DIM > *  pPde,
BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 1 > *  pBoundaryConditions,
unsigned  numQuadPoints = 2 
) [inline]

Constructor - takes in the mesh, pde and boundary conditions container to be solved. Can also define the number of quad points (in each dimension), the default value of which is 2.

Parameters:
pMesh pointer to the mesh
pPde pointer to the PDE
pBoundaryConditions pointer to the boundary conditions
numQuadPoints number of quadrature points (defaults to 2)

Definition at line 34 of file SimpleNonlinearEllipticAssembler.cpp.

References SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde, AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::SetBoundaryConditionsContainer(), and AbstractStaticAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, true, SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM > >::SetMesh().

Member Function Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
c_matrix< double, 1 *(ELEMENT_DIM+1), 1 *(ELEMENT_DIM+1)> SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::ComputeMatrixTerm ( c_vector< double, ELEMENT_DIM+1 > &  rPhi,
c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &  rGradPhi,
ChastePoint< SPACE_DIM > &  rX,
c_vector< double, 1 > &  rU,
c_matrix< double, 1, SPACE_DIM > &  rGradU,
Element< ELEMENT_DIM, SPACE_DIM > *  pElement 
) [inline, private, virtual]

This method returns the matrix to be added to element stiffness matrix for a given gauss point. The arguments are the bases, bases gradients, x and current solution computed at the Gauss point. The returned matrix will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).

Parameters:
rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases
rGradPhi Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i)
rX The point in space
rU The unknown as a vector, u(i) = u_i
rGradU The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j)
pElement Pointer to the element

Todo:
#1298 Should these be SPACE_DIM??

Definition at line 58 of file SimpleNonlinearEllipticAssembler.cpp.

References SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
c_vector< double, 1 *ELEMENT_DIM > SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::ComputeVectorSurfaceTerm ( const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &  rSurfaceElement,
c_vector< double, ELEMENT_DIM > &  rPhi,
ChastePoint< SPACE_DIM > &  rX 
) [inline, private, virtual]

This method returns the vector to be added to element stiffness vector for a given gauss point in BoundaryElement. The arguments are the bases, x and current solution computed at the Gauss point. The returned vector will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).

Parameters:
rSurfaceElement the element which is being considered.
rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases
rX The point in space

Implements AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >.

Definition at line 127 of file SimpleNonlinearEllipticAssembler.cpp.

References AbstractAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpBoundaryConditions.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
c_vector< double, 1 *(ELEMENT_DIM+1)> SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::ComputeVectorTerm ( c_vector< double, ELEMENT_DIM+1 > &  rPhi,
c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &  rGradPhi,
ChastePoint< SPACE_DIM > &  rX,
c_vector< double, 1 > &  rU,
c_matrix< double, 1, SPACE_DIM > &  rGradU,
Element< ELEMENT_DIM, SPACE_DIM > *  pElement 
) [inline, private, virtual]

This method returns the vector to be added to element stiffness vector for a given gauss point. The arguments are the bases, x and current solution computed at the Gauss point. The returned vector will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).

Parameters:
rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases
rGradPhi Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i)
rX The point in space
rU The unknown as a vector, u(i) = u_i
rGradU The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j)
pElement Pointer to the element

Definition at line 93 of file SimpleNonlinearEllipticAssembler.cpp.

References SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde.

Member Data Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
const unsigned SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::E_DIM = ELEMENT_DIM [static]

The element dimension (to save typing).

Definition at line 53 of file SimpleNonlinearEllipticAssembler.hpp.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
AbstractNonlinearEllipticPde<SPACE_DIM>* SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde [private]

The PDE to be solved.

Definition at line 67 of file SimpleNonlinearEllipticAssembler.hpp.

Referenced by SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::ComputeMatrixTerm(), SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::ComputeVectorTerm(), and SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::SimpleNonlinearEllipticAssembler().

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
const unsigned SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::P_DIM = 1u [static]

The problem dimension (to save typing).

Definition at line 55 of file SimpleNonlinearEllipticAssembler.hpp.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
const unsigned SimpleNonlinearEllipticAssembler< ELEMENT_DIM, SPACE_DIM >::S_DIM = SPACE_DIM [static]

The space dimension (to save typing).

Definition at line 54 of file SimpleNonlinearEllipticAssembler.hpp.

The documentation for this class was generated from the following files:
Generated by  doxygen 1.6.2