AbstractIncompressibleMaterialLaw< DIM > Class Template Reference
#include <AbstractIncompressibleMaterialLaw.hpp>
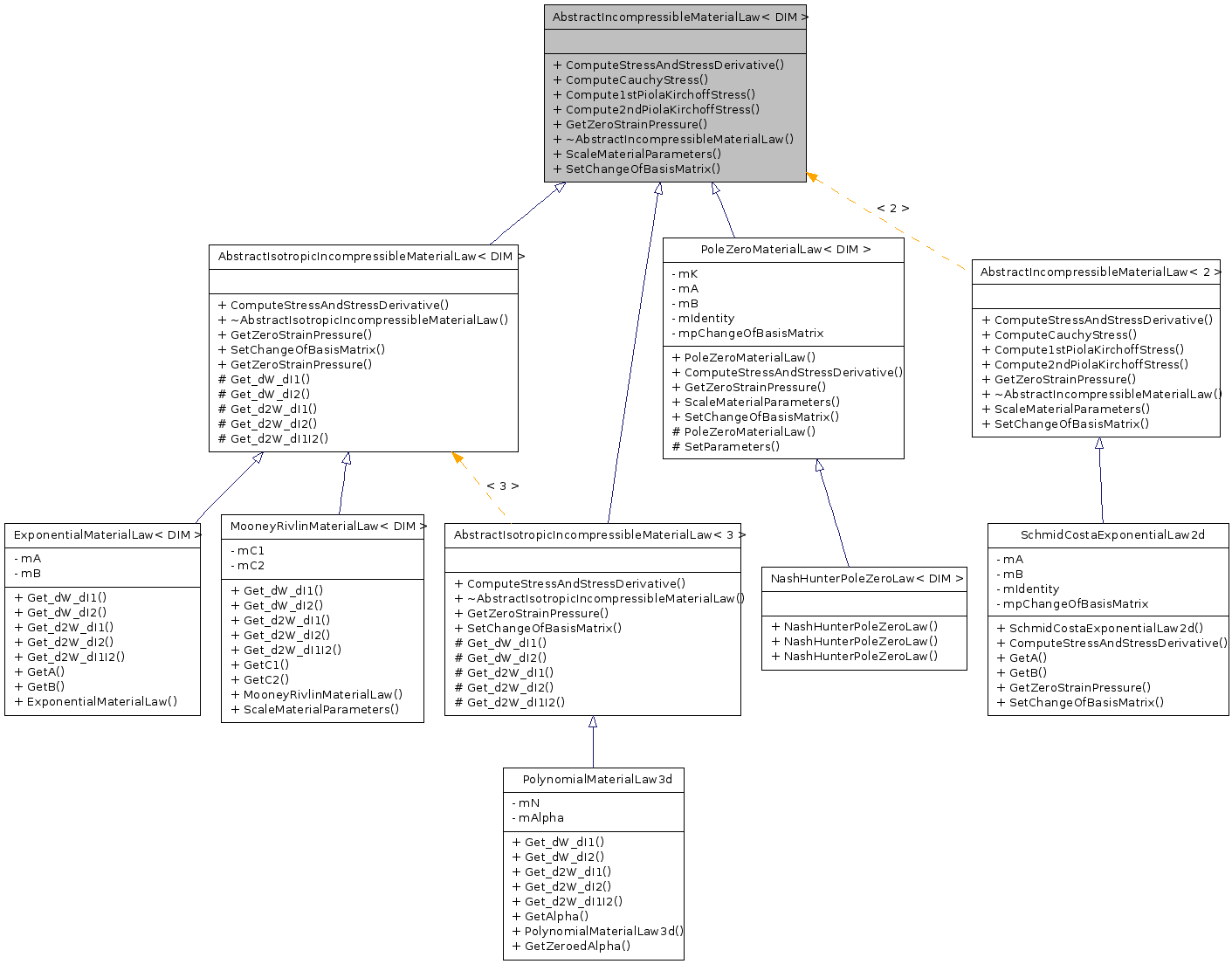
Public Member Functions | |
| virtual void | ComputeStressAndStressDerivative (c_matrix< double, DIM, DIM > &rC, c_matrix< double, DIM, DIM > &rInvC, double pressure, c_matrix< double, DIM, DIM > &rT, FourthOrderTensor< DIM, DIM, DIM, DIM > &rDTdE, bool computeDTdE)=0 |
| void | ComputeCauchyStress (c_matrix< double, DIM, DIM > &rF, double pressure, c_matrix< double, DIM, DIM > &rSigma) |
| void | Compute1stPiolaKirchoffStress (c_matrix< double, DIM, DIM > &rF, double pressure, c_matrix< double, DIM, DIM > &rS) |
| void | Compute2ndPiolaKirchoffStress (c_matrix< double, DIM, DIM > &rC, double pressure, c_matrix< double, DIM, DIM > &rT) |
| virtual double | GetZeroStrainPressure ()=0 |
| virtual | ~AbstractIncompressibleMaterialLaw () |
| virtual void | ScaleMaterialParameters (double scaleFactor) |
| virtual void | SetChangeOfBasisMatrix (c_matrix< double, DIM, DIM > &rChangeOfBasisMatrix)=0 |
Detailed Description
template<unsigned DIM>
class AbstractIncompressibleMaterialLaw< DIM >
AbstractIncompressibleMaterialLawAn incompressible hyperelastic material law for finite elastiticy
The law is given by a strain energy function W(E), where E is the strain, such that the stress T = dW/dE
Definition at line 48 of file AbstractIncompressibleMaterialLaw.hpp.
Constructor & Destructor Documentation
| AbstractIncompressibleMaterialLaw< DIM >::~AbstractIncompressibleMaterialLaw | ( | ) | [inline, virtual] |
Destructor.
Definition at line 32 of file AbstractIncompressibleMaterialLaw.cpp.
Member Function Documentation
| virtual void AbstractIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative | ( | c_matrix< double, DIM, DIM > & | rC, | |
| c_matrix< double, DIM, DIM > & | rInvC, | |||
| double | pressure, | |||
| c_matrix< double, DIM, DIM > & | rT, | |||
| FourthOrderTensor< DIM, DIM, DIM, DIM > & | rDTdE, | |||
| bool | computeDTdE | |||
| ) | [pure virtual] |
Compute the (2nd Piola Kirchoff) stress T and the stress derivative dT/dE for a given strain.
NOTE: the strain E is not expected to be passed in, instead the Lagrangian deformation tensor C is required (recall, E = 0.5(C-I))
dTdE is a fourth-order tensor, where dTdE(M,N,P,Q) = dT^{MN}/dE_{PQ}
- Parameters:
-
rC The Lagrangian deformation tensor (F^T F) rInvC The inverse of C. Should be computed by the user. pressure the current pressure rT the stress will be returned in this parameter rDTdE the stress derivative will be returned in this parameter, assuming the final parameter is true computeDTdE a boolean flag saying whether the stress derivative is required or not.
Implemented in AbstractIsotropicIncompressibleMaterialLaw< DIM >, PoleZeroMaterialLaw< DIM >, and AbstractIsotropicIncompressibleMaterialLaw< 3 >.
Referenced by AbstractIncompressibleMaterialLaw< DIM >::Compute1stPiolaKirchoffStress(), AbstractIncompressibleMaterialLaw< DIM >::Compute2ndPiolaKirchoffStress(), AbstractIncompressibleMaterialLaw< DIM >::ComputeCauchyStress(), NonlinearElasticitySolver< DIM >::ComputeStressAndStressDerivative(), and AbstractCardiacMechanicsSolver< DIM >::ComputeStressAndStressDerivative().
| void AbstractIncompressibleMaterialLaw< DIM >::ComputeCauchyStress | ( | c_matrix< double, DIM, DIM > & | rF, | |
| double | pressure, | |||
| c_matrix< double, DIM, DIM > & | rSigma | |||
| ) | [inline] |
Compute the Cauchy stress (the true stress), given the deformation gradient F and the pressure. The Cauchy stress is given by
sigma^{ij} = (1/detF) F^i_M T^{MN} F^j_N
where T is the 2nd Piola Kirchoff stress, dW/dE
- Parameters:
-
rF the deformation gradient pressure the pressure rSigma an empty matrix, which will be filled in with the Cauchy stress
Definition at line 37 of file AbstractIncompressibleMaterialLaw.cpp.
References AbstractIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative(), Determinant(), and Inverse().
| void AbstractIncompressibleMaterialLaw< DIM >::Compute1stPiolaKirchoffStress | ( | c_matrix< double, DIM, DIM > & | rF, | |
| double | pressure, | |||
| c_matrix< double, DIM, DIM > & | rS | |||
| ) | [inline] |
Compute the 1st Piola Kirchoff stress, given the deformation gradient F and the pressure. The 1st Piola Kirchoff stress given by
S^{Mi} = T^{MN} F^i_M,
where T is the 2nd PK stress, dW/dE.
Note that this stress is not symmetric and the least useful of the three stresses.
- Parameters:
-
rF the deformation gradient pressure the pressure rS an empty matrix, which will be filled in with the stress
Definition at line 73 of file AbstractIncompressibleMaterialLaw.cpp.
References AbstractIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative(), and Inverse().
| void AbstractIncompressibleMaterialLaw< DIM >::Compute2ndPiolaKirchoffStress | ( | c_matrix< double, DIM, DIM > & | rC, | |
| double | pressure, | |||
| c_matrix< double, DIM, DIM > & | rT | |||
| ) | [inline] |
Compute the 2nd Piola Kirchoff stress, given the deformation tensor C and the pressure. The 2nd Piola Kirchoff stress given by
T^{MN} = dW/dE_{MN} = 2dW/dC_{MN}
- Parameters:
-
rC the Lagrange deformation tensor (C=F^T F), *not* F, and *not* E pressure the pressure rT an empty matrix, which will be filled in with the stress
Definition at line 90 of file AbstractIncompressibleMaterialLaw.cpp.
References AbstractIncompressibleMaterialLaw< DIM >::ComputeStressAndStressDerivative(), and Inverse().
| virtual double AbstractIncompressibleMaterialLaw< DIM >::GetZeroStrainPressure | ( | ) | [pure virtual] |
Get the pressure corresponding to E=0, ie C=identity
Implemented in AbstractIsotropicIncompressibleMaterialLaw< DIM >, PoleZeroMaterialLaw< DIM >, SchmidCostaExponentialLaw2d, AbstractIsotropicIncompressibleMaterialLaw< 3 >, and AbstractIsotropicIncompressibleMaterialLaw< DIM >.
| void AbstractIncompressibleMaterialLaw< DIM >::ScaleMaterialParameters | ( | double | scaleFactor | ) | [inline, virtual] |
Set a scale factor by which (dimensional) material parameters are scaled. This method can be optionally implemented in the child class; if no implementation is made an exception is thrown. A scale factor may be used/needed to improve GMRES convergence. Note that is a material law is scaled like this any dimensionally equivalent terms (eg gravity, tractions, active tensions) must also be scaled. Also, computed pressure will come out scaled.
- Parameters:
-
scaleFactor the scale factor
Reimplemented in MooneyRivlinMaterialLaw< DIM >, and PoleZeroMaterialLaw< DIM >.
Definition at line 102 of file AbstractIncompressibleMaterialLaw.cpp.
References EXCEPTION.
| virtual void AbstractIncompressibleMaterialLaw< DIM >::SetChangeOfBasisMatrix | ( | c_matrix< double, DIM, DIM > & | rChangeOfBasisMatrix | ) | [pure virtual] |
Some material laws (eg pole-zero) may have prefered directions (eg fibre direction), but be implemented to assume the prefered directions are parallel to the X-axis etc. Call this with the change of basis matrix and C will be transformed from the Euclidean coordinate system to the appropriate coordinate system before used to calculate T, which will then be transformed from the appropriate coordinate system back to the Euclidean coordinate system before being returned, as will dTdE
- Parameters:
-
rChangeOfBasisMatrix Change of basis matrix.
Implemented in AbstractIsotropicIncompressibleMaterialLaw< DIM >, PoleZeroMaterialLaw< DIM >, and AbstractIsotropicIncompressibleMaterialLaw< 3 >.
Referenced by AbstractCardiacMechanicsSolver< DIM >::ComputeStressAndStressDerivative().
The documentation for this class was generated from the following files:
- pde/src/problem/common/AbstractIncompressibleMaterialLaw.hpp
- pde/src/problem/common/AbstractIncompressibleMaterialLaw.cpp
 1.5.5
1.5.5