CompressibleExponentialLaw< DIM > Class Template Reference
#include <CompressibleExponentialLaw.hpp>

Public Member Functions | |
| CompressibleExponentialLaw () | |
| void | ComputeStressAndStressDerivative (c_matrix< double, DIM, DIM > &rC, c_matrix< double, DIM, DIM > &rInvC, double pressure, c_matrix< double, DIM, DIM > &rT, FourthOrderTensor< DIM, DIM, DIM, DIM > &rDTdE, bool computeDTdE) |
| double | GetA () |
| std::vector< std::vector < double > > | GetB () |
| double | GetCompressibilityParam () |
Private Attributes | |
| double | mA |
| std::vector< std::vector < double > > | mB |
| double | mCompressibilityParam |
| c_matrix< double, DIM, DIM > | mIdentity |
Detailed Description
template<unsigned DIM>
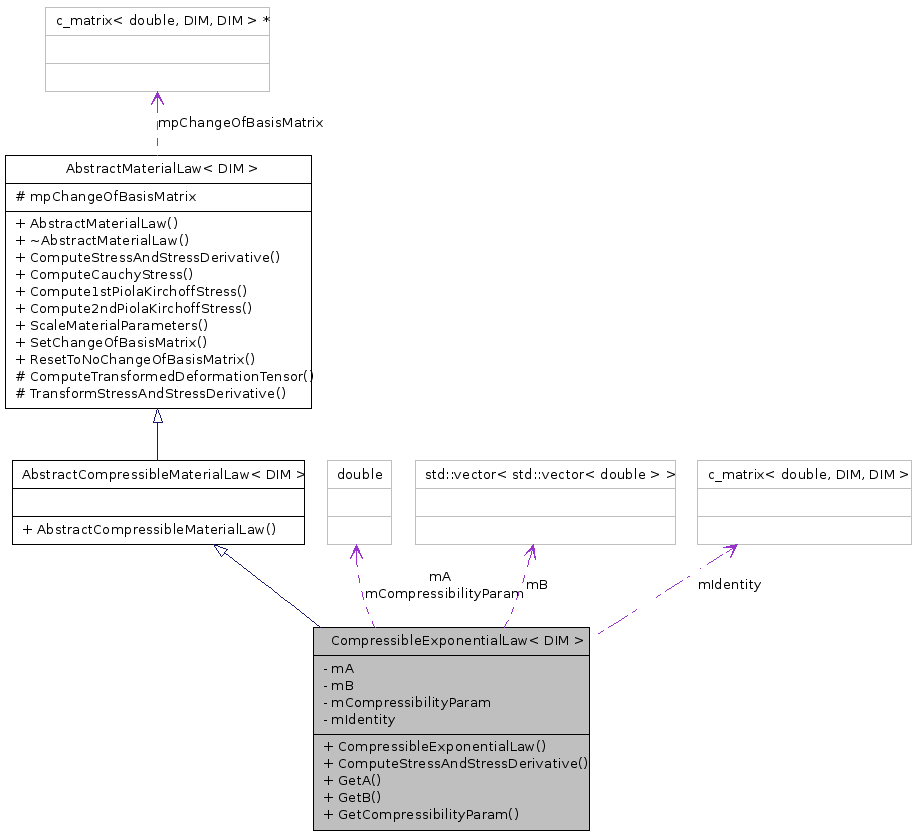
class CompressibleExponentialLaw< DIM >
The compressible exponential material law implemented inUysk, Effect of Laminar Orthotropic Myofiber Architecture on Regional Stress and Strain in the Canine Left Ventricle, Journal of Elasticity, 2000.
W = a[exp(Q)-1]/2 + C (J ln(J) - J + 1) where Q = sum b_{MN} E_{MN}^2
The exponential term is the same form as in the SchmidCosta law, although the parameters here are those given in the paper cited above, not the same as in the SchmidCosta class.
Note, by default, the fibre direction is assumed to be THE X-DIRECTION, and the sheet direction the Y-DIRECTION (ie sheets in the XY plane). Call SetChangeOfBasisMatrix() before ComputeStressAndStressDerivative(), with the matrix P = [fibre_vec, sheet_vec, normal_vec] if this is not the case.
Definition at line 53 of file CompressibleExponentialLaw.hpp.
Constructor & Destructor Documentation
| CompressibleExponentialLaw< DIM >::CompressibleExponentialLaw | ( | ) | [inline] |
Constructor.
Definition at line 34 of file CompressibleExponentialLaw.cpp.
References CompressibleExponentialLaw< DIM >::mA, CompressibleExponentialLaw< DIM >::mB, CompressibleExponentialLaw< DIM >::mCompressibilityParam, and CompressibleExponentialLaw< DIM >::mIdentity.
Member Function Documentation
| void CompressibleExponentialLaw< DIM >::ComputeStressAndStressDerivative | ( | c_matrix< double, DIM, DIM > & | rC, | |
| c_matrix< double, DIM, DIM > & | rInvC, | |||
| double | pressure, | |||
| c_matrix< double, DIM, DIM > & | rT, | |||
| FourthOrderTensor< DIM, DIM, DIM, DIM > & | rDTdE, | |||
| bool | computeDTdE | |||
| ) | [inline, virtual] |
Compute the (2nd Piola Kirchoff) stress T and the stress derivative dT/dE for a given strain.
NOTE: the strain E is not expected to be passed in, instead the Lagrangian deformation tensor C is required (recall, E = 0.5(C-I))
dT/dE is a fourth-order tensor, where dT/dE[M][N][P][Q] = dT^{MN}/dE_{PQ}
- Parameters:
-
rC The Lagrangian deformation tensor (F^T F) rInvC The inverse of C. Should be computed by the user. (Change this?) pressure the current pressure rT the stress will be returned in this parameter rDTdE the stress derivative will be returned in this parameter, assuming the final parameter is true computeDTdE a boolean flag saying whether the stress derivative is required or not.
Implements AbstractMaterialLaw< DIM >.
Definition at line 76 of file CompressibleExponentialLaw.cpp.
References AbstractMaterialLaw< DIM >::ComputeTransformedDeformationTensor(), Determinant(), CompressibleExponentialLaw< DIM >::mA, CompressibleExponentialLaw< DIM >::mB, CompressibleExponentialLaw< DIM >::mCompressibilityParam, CompressibleExponentialLaw< DIM >::mIdentity, AbstractMaterialLaw< DIM >::TransformStressAndStressDerivative(), and FourthOrderTensor< DIM1, DIM2, DIM3, DIM4 >::Zero().
| double CompressibleExponentialLaw< DIM >::GetA | ( | ) | [inline] |
Get method for the parameter a
Definition at line 98 of file CompressibleExponentialLaw.hpp.
References CompressibleExponentialLaw< DIM >::mA.
| std::vector<std::vector<double> > CompressibleExponentialLaw< DIM >::GetB | ( | ) | [inline] |
Get method for the parameter b (the values which multiply the strains in Q)
Definition at line 104 of file CompressibleExponentialLaw.hpp.
References CompressibleExponentialLaw< DIM >::mB.
| double CompressibleExponentialLaw< DIM >::GetCompressibilityParam | ( | ) | [inline] |
Get method for compressibility parameter
Definition at line 110 of file CompressibleExponentialLaw.hpp.
References CompressibleExponentialLaw< DIM >::mCompressibilityParam.
Member Data Documentation
double CompressibleExponentialLaw< DIM >::mA [private] |
Parameter a. (kPa)
Definition at line 57 of file CompressibleExponentialLaw.hpp.
Referenced by CompressibleExponentialLaw< DIM >::CompressibleExponentialLaw(), CompressibleExponentialLaw< DIM >::ComputeStressAndStressDerivative(), and CompressibleExponentialLaw< DIM >::GetA().
std::vector<std::vector<double> > CompressibleExponentialLaw< DIM >::mB [private] |
Matrix of parameters b (dimensionless).
Definition at line 60 of file CompressibleExponentialLaw.hpp.
Referenced by CompressibleExponentialLaw< DIM >::CompressibleExponentialLaw(), CompressibleExponentialLaw< DIM >::ComputeStressAndStressDerivative(), and CompressibleExponentialLaw< DIM >::GetB().
double CompressibleExponentialLaw< DIM >::mCompressibilityParam [private] |
Compressibility parameter, c in W = a[exp(Q)-1]/2 + c (J ln(J) - J + 1)
Definition at line 63 of file CompressibleExponentialLaw.hpp.
Referenced by CompressibleExponentialLaw< DIM >::CompressibleExponentialLaw(), CompressibleExponentialLaw< DIM >::ComputeStressAndStressDerivative(), and CompressibleExponentialLaw< DIM >::GetCompressibilityParam().
c_matrix<double,DIM,DIM> CompressibleExponentialLaw< DIM >::mIdentity [private] |
identity matrix.
Definition at line 66 of file CompressibleExponentialLaw.hpp.
Referenced by CompressibleExponentialLaw< DIM >::CompressibleExponentialLaw(), and CompressibleExponentialLaw< DIM >::ComputeStressAndStressDerivative().
The documentation for this class was generated from the following files:
- pde/src/problem/CompressibleExponentialLaw.hpp
- pde/src/problem/CompressibleExponentialLaw.cpp
 1.5.5
1.5.5