SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM > Class Template Reference
#include <SimpleNonlinearEllipticSolver.hpp>

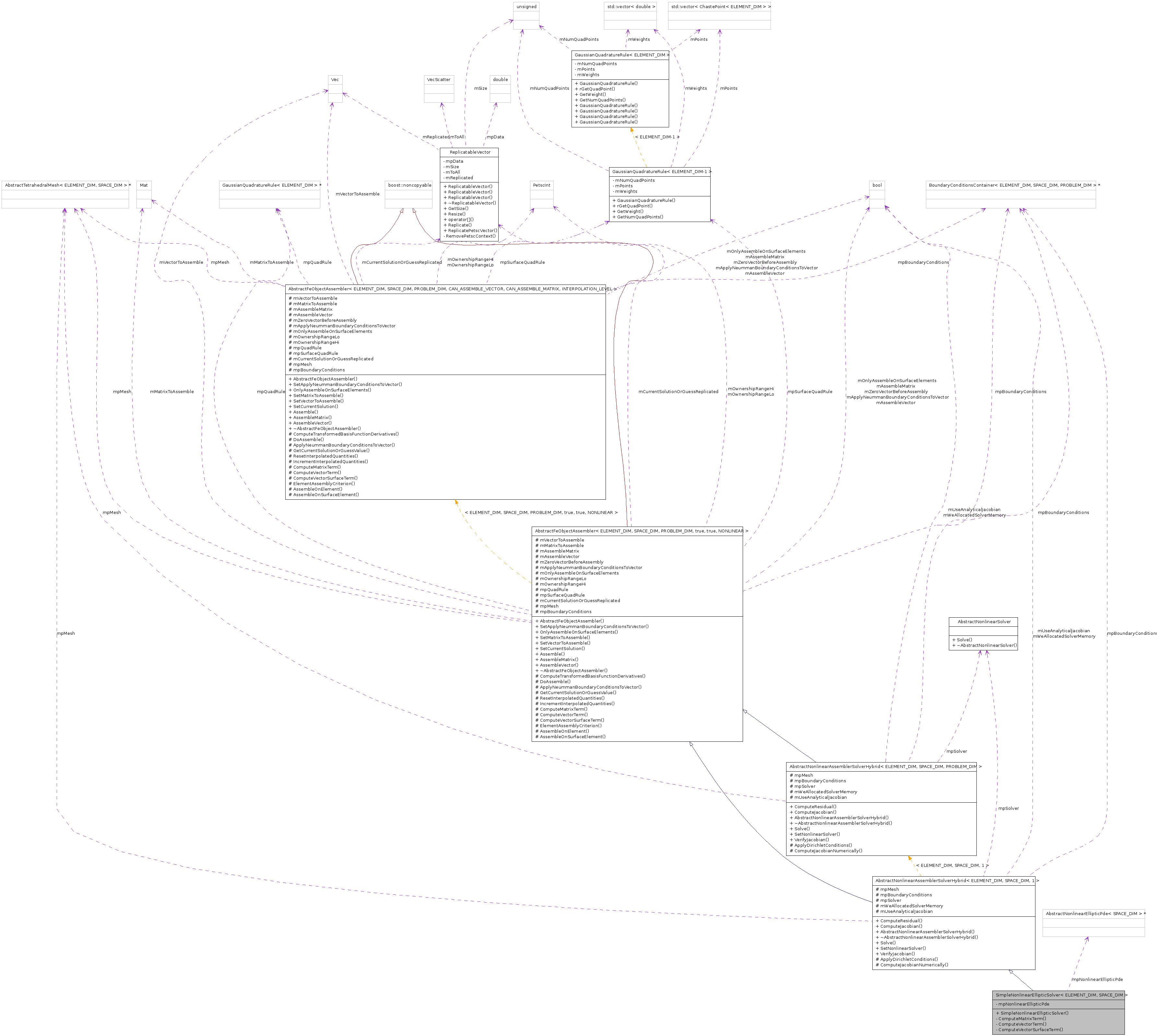
Public Member Functions | |
| SimpleNonlinearEllipticSolver (AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *pMesh, AbstractNonlinearEllipticPde< SPACE_DIM > *pPde, BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 1 > *pBoundaryConditions, unsigned numQuadPoints=2) | |
Private Member Functions | |
| virtual c_matrix< double, 1 *(ELEMENT_DIM+1), 1 *(ELEMENT_DIM+1)> | ComputeMatrixTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, 1 > &rU, c_matrix< double, 1, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement) |
| virtual c_vector< double, 1 *(ELEMENT_DIM+1)> | ComputeVectorTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, 1 > &rU, c_matrix< double, 1, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement) |
| virtual c_vector< double, 1 *ELEMENT_DIM > | ComputeVectorSurfaceTerm (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, ELEMENT_DIM > &rPhi, ChastePoint< SPACE_DIM > &rX) |
Private Attributes | |
| AbstractNonlinearEllipticPde < SPACE_DIM > * | mpNonlinearEllipticPde |
Detailed Description
template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
class SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >
Solver of nonlinear elliptic PDEs
Definition at line 39 of file SimpleNonlinearEllipticSolver.hpp.
Constructor & Destructor Documentation
| SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::SimpleNonlinearEllipticSolver | ( | AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > * | pMesh, | |
| AbstractNonlinearEllipticPde< SPACE_DIM > * | pPde, | |||
| BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 1 > * | pBoundaryConditions, | |||
| unsigned | numQuadPoints = 2 | |||
| ) | [inline] |
Constructor
- Parameters:
-
pMesh pointer to the mesh pPde pointer to the PDE pBoundaryConditions pointer to the boundary conditions numQuadPoints number of quadrature points in each dimension to use per element (defaults to 2)
Definition at line 107 of file SimpleNonlinearEllipticSolver.cpp.
Member Function Documentation
| c_matrix< double, 1 *(ELEMENT_DIM+1), 1 *(ELEMENT_DIM+1)> SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeMatrixTerm | ( | c_vector< double, ELEMENT_DIM+1 > & | rPhi, | |
| c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > & | rGradPhi, | |||
| ChastePoint< SPACE_DIM > & | rX, | |||
| c_vector< double, 1 > & | rU, | |||
| c_matrix< double, 1, SPACE_DIM > & | rGradU, | |||
| Element< ELEMENT_DIM, SPACE_DIM > * | pElement | |||
| ) | [inline, private, virtual] |
This method returns the matrix to be added to element stiffness matrix for a given gauss point. The arguments are the bases, bases gradients, x and current solution computed at the Gauss point. The returned matrix will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).
- Parameters:
-
rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases rGradPhi Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i) rX The point in space rU The unknown as a vector, u(i) = u_i rGradU The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j) pElement Pointer to the element
Definition at line 33 of file SimpleNonlinearEllipticSolver.cpp.
References SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde.
| c_vector< double, 1 *(ELEMENT_DIM+1)> SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeVectorTerm | ( | c_vector< double, ELEMENT_DIM+1 > & | rPhi, | |
| c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > & | rGradPhi, | |||
| ChastePoint< SPACE_DIM > & | rX, | |||
| c_vector< double, 1 > & | rU, | |||
| c_matrix< double, 1, SPACE_DIM > & | rGradU, | |||
| Element< ELEMENT_DIM, SPACE_DIM > * | pElement | |||
| ) | [inline, private, virtual] |
This method returns the vector to be added to element stiffness vector for a given gauss point. The arguments are the bases, x and current solution computed at the Gauss point. The returned vector will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).
- Parameters:
-
rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases rGradPhi Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i) rX The point in space rU The unknown as a vector, u(i) = u_i rGradU The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j) pElement Pointer to the element
Definition at line 66 of file SimpleNonlinearEllipticSolver.cpp.
References SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde.
| c_vector< double, 1 *ELEMENT_DIM > SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeVectorSurfaceTerm | ( | const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > & | rSurfaceElement, | |
| c_vector< double, ELEMENT_DIM > & | rPhi, | |||
| ChastePoint< SPACE_DIM > & | rX | |||
| ) | [inline, private, virtual] |
This method returns the vector to be added to element stiffness vector for a given gauss point in BoundaryElement. The arguments are the bases, x and current solution computed at the Gauss point. The returned vector will be multiplied by the gauss weight and jacobian determinent and added to the element stiffness matrix (see AssembleOnElement()).
- Parameters:
-
rSurfaceElement the element which is being considered. rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases rX The point in space
Reimplemented from AbstractFeObjectAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, true, true, NONLINEAR >.
Definition at line 96 of file SimpleNonlinearEllipticSolver.cpp.
References AbstractNonlinearAssemblerSolverHybrid< ELEMENT_DIM, SPACE_DIM, 1 >::mpBoundaryConditions.
Member Data Documentation
AbstractNonlinearEllipticPde<SPACE_DIM>* SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde [private] |
The PDE to be solved.
Definition at line 43 of file SimpleNonlinearEllipticSolver.hpp.
Referenced by SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeMatrixTerm(), and SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeVectorTerm().
The documentation for this class was generated from the following files:
- pde/src/solver/SimpleNonlinearEllipticSolver.hpp
- pde/src/solver/SimpleNonlinearEllipticSolver.cpp
 1.5.5
1.5.5