NhsModelWithBackwardSolver Class Reference

#include <NhsModelWithBackwardSolver.hpp>

Inheritance diagram for NhsModelWithBackwardSolver:

Collaboration diagram for NhsModelWithBackwardSolver:

List of all members.

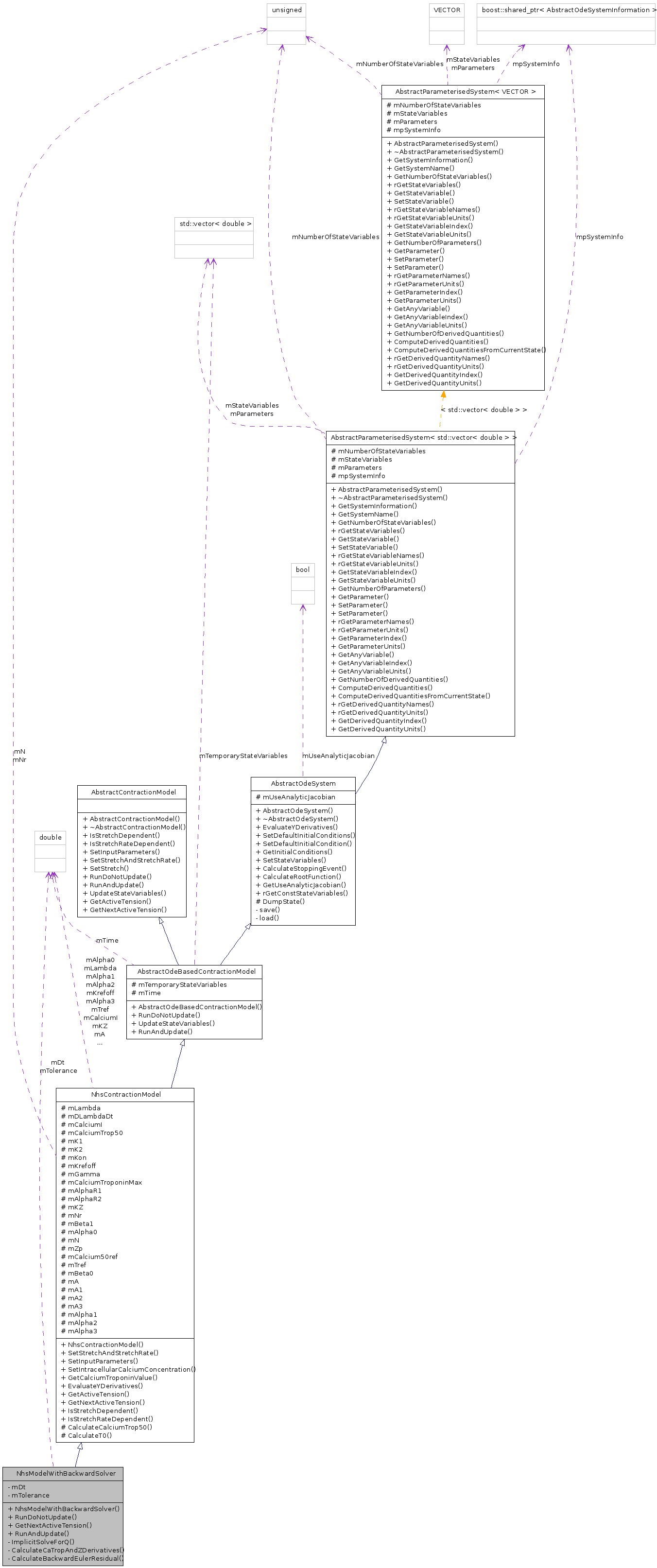
Public Member Functions

NhsModelWithBackwardSolver ()

void RunDoNotUpdate (double startTime, double endTime, double timestep)

double GetNextActiveTension ()

void RunAndUpdate (double startTime, double endTime, double timestep)

Private Member Functions

double ImplicitSolveForQ ()

void CalculateCaTropAndZDerivatives (double calciumTroponin, double z, double Q, double &dCaTrop, double &dz)

void CalculateBackwardEulerResidual (double calciumTroponin, double z, double Q, double &residualComponent1, double &residualComponent2)

Private Attributes

double mDt

Static Private Attributes

static const double mTolerance = 1e-10

Detailed Description

The full backward Euler method on the NHS system compute the solution w^{n+1} in R^5 by: w^{n+1} - dt g(w^{n+1}) = w^n where the ODE system is dw/dt = g(w).

This would involve solving a 5d nonlinear system at each timestep. However, only g1 and g2 (ie dCatrop/dt and dz/dt) are nonlinear, g3, g4 and g5 (corresponding to dQi/dt) are linear and uncoupled. Therefore the backward euler solutions of Q1,Q2,Q3 can be computed immediately, leaving a 2D nonlinear system to be solved using newton's method

Definition at line 49 of file NhsModelWithBackwardSolver.hpp.

Constructor & Destructor Documentation

NhsModelWithBackwardSolver::NhsModelWithBackwardSolver ( )

Constructor

Definition at line 103 of file NhsModelWithBackwardSolver.cpp.

References AbstractOdeBasedContractionModel::mTemporaryStateVariables.

Member Function Documentation

double NhsModelWithBackwardSolver::ImplicitSolveForQ ( ) [private]

Solve for Q1,Q2,Q3 (and therefore Q) implicitly using backward euler. These can be done directly as the rhs is linear in Qi

Returns:: Q=Q1+Q2+Q3

Definition at line 38 of file NhsModelWithBackwardSolver.cpp.

References NhsContractionModel::mA1, NhsContractionModel::mA2, NhsContractionModel::mA3, NhsContractionModel::mAlpha1, NhsContractionModel::mAlpha2, NhsContractionModel::mAlpha3, NhsContractionModel::mDLambdaDt, mDt, and AbstractOdeBasedContractionModel::mTemporaryStateVariables.

Referenced by RunDoNotUpdate().

void NhsModelWithBackwardSolver::CalculateCaTropAndZDerivatives	(	double	calciumTroponin,
		double	z,
		double	Q,
		double &	dCaTrop,
		double &	dz
	)			`[private]`

The same as EvaluateYDerivatives in NhsContractionModel, but doesn't use std::vectors (for efficiency, and because this class is hardcoded and hand-optimised for backward euler), and just returns the derivatives of the first two components

Parameters:

	calciumTroponin	Calcium troponin
	z	z
	Q	Q=Q1+Q2+Q3
	dCaTrop	the returned value of dCaTrop/dt
	dz	the returned value of dz/dt

Definition at line 47 of file NhsModelWithBackwardSolver.cpp.

References NhsContractionModel::CalculateT0(), EXCEPTION, NhsContractionModel::mA, NhsContractionModel::mAlpha0, NhsContractionModel::mAlphaR1, NhsContractionModel::mAlphaR2, NhsContractionModel::mCalciumI, NhsContractionModel::mCalciumTrop50, NhsContractionModel::mCalciumTroponinMax, NhsContractionModel::mGamma, NhsContractionModel::mKon, NhsContractionModel::mKrefoff, NhsContractionModel::mKZ, NhsContractionModel::mN, NhsContractionModel::mNr, and NhsContractionModel::mTref.

Referenced by CalculateBackwardEulerResidual().

void NhsModelWithBackwardSolver::CalculateBackwardEulerResidual	(	double	calciumTroponin,
		double	z,
		double	Q,
		double &	residualComponent1,
		double &	residualComponent2
	)			`[private]`

Compute the residual function for the 2D nonlinear system when Backward Euler is used The backward Euler discretisation is: w^{n+1} - dt g(w^{n+1}) = w^n where: w = (ca_trop, z) and the ODE system is: dw/dt = g(w)

so the residual is: f = w^{n+1} - dt g(w^{n+1}) - w^n

Parameters:

	calciumTroponin	Current guess for Ca_trop value
	z	current guess for z
	Q	= Q1+Q2+Q3, where Qi already computed at next timestep
	residualComponent1	Returned value - first component of residual
	residualComponent2	Returned value - second component of residual

Definition at line 90 of file NhsModelWithBackwardSolver.cpp.

References CalculateCaTropAndZDerivatives(), mDt, and AbstractOdeBasedContractionModel::mTemporaryStateVariables.

Referenced by RunDoNotUpdate().

void NhsModelWithBackwardSolver::RunDoNotUpdate	(	double	startTime,
		double	endTime,
		double	timestep
	)			`[virtual]`

Solves for the new state variables at the given end time using the implicit method. Note that the internal state variables are not altered, the solution is saved instead. Call UpdateStateVariables() to update, and GetNextActiveTension() to get the solved active tension

The state variables are not updated because this solve will be called as part of the newton iteration (ie guess stretch, see what the new active tension is) in a fully implicit method.

Note: overloaded from the method in AbstractOdeBasedContractionModel, which just does a simple Euler solve

Parameters:

	startTime
	endTime
	timestep

Reimplemented from AbstractOdeBasedContractionModel.

Definition at line 110 of file NhsModelWithBackwardSolver.cpp.

References TimeStepper::AdvanceOneTimeStep(), CalculateBackwardEulerResidual(), ImplicitSolveForQ(), TimeStepper::IsTimeAtEnd(), mDt, AbstractParameterisedSystem< std::vector< double > >::mStateVariables, AbstractOdeBasedContractionModel::mTemporaryStateVariables, and mTolerance.

Referenced by RunAndUpdate().

double NhsModelWithBackwardSolver::GetNextActiveTension ( ) [virtual]

Get the active tension corresponding to the stored state variables computed from the last RunDoNotUpdate(), ie the active tension at the next time. Note that calling GetActiveTension() on the base class will use the internal state variables and return the active tension at the last time, if RunDoNotUpdate() has been called but UpdateStateVariables() has not

Reimplemented from NhsContractionModel.

Definition at line 179 of file NhsModelWithBackwardSolver.cpp.

References NhsContractionModel::CalculateT0(), NhsContractionModel::mA, and AbstractOdeBasedContractionModel::mTemporaryStateVariables.

void NhsModelWithBackwardSolver::RunAndUpdate	(	double	startTime,
		double	endTime,
		double	timestep
	)			`[virtual]`

Overload the RunAndUpdate() method too, as that would use the base class's default (euler) solver

Parameters:

	startTime
	endTime
	timestep

Reimplemented from AbstractOdeBasedContractionModel.

Definition at line 194 of file NhsModelWithBackwardSolver.cpp.

References RunDoNotUpdate(), and AbstractOdeBasedContractionModel::UpdateStateVariables().

Member Data Documentation

const double NhsModelWithBackwardSolver::mTolerance = 1e-10 [static, private]

Tolerance for solving nonlinear system which require newton's method

Definition at line 53 of file NhsModelWithBackwardSolver.hpp.

Referenced by RunDoNotUpdate().

double NhsModelWithBackwardSolver::mDt [private]

Timestep for the ODEs solving

Definition at line 56 of file NhsModelWithBackwardSolver.hpp.

Referenced by CalculateBackwardEulerResidual(), ImplicitSolveForQ(), and RunDoNotUpdate().

The documentation for this class was generated from the following files:

heart/src/odes/contractionmodels/NhsModelWithBackwardSolver.hpp
heart/src/odes/contractionmodels/NhsModelWithBackwardSolver.cpp


Public Member Functions
	NhsModelWithBackwardSolver ()
void	RunDoNotUpdate (double startTime, double endTime, double timestep)
double	GetNextActiveTension ()
void	RunAndUpdate (double startTime, double endTime, double timestep)
Private Member Functions
double	ImplicitSolveForQ ()
void	CalculateCaTropAndZDerivatives (double calciumTroponin, double z, double Q, double &dCaTrop, double &dz)
void	CalculateBackwardEulerResidual (double calciumTroponin, double z, double Q, double &residualComponent1, double &residualComponent2)
Private Attributes
double	mDt
Static Private Attributes
static const double	mTolerance = 1e-10