AbstractNonlinearElasticitySolver< DIM > Class Template Reference

#include <AbstractNonlinearElasticitySolver.hpp>

Inherited by CompressibleNonlinearElasticitySolver< DIM >, and IncompressibleNonlinearElasticitySolver< DIM >.

Collaboration diagram for AbstractNonlinearElasticitySolver< DIM >:

Public Member Functions
	AbstractNonlinearElasticitySolver (QuadraticMesh< DIM > &rQuadMesh, SolidMechanicsProblemDefinition< DIM > &rProblemDefinition, std::string outputDirectory, CompressibilityType compressibilityType)
virtual	~AbstractNonlinearElasticitySolver ()
void	Solve (double tol=-1.0, unsigned maxNumNewtonIterations=INT_MAX, bool quitIfNoConvergence=true)
void	WriteCurrentDeformation (std::string fileName, int counterToAppend=-1)
unsigned	GetNumNewtonIterations ()
void	SetWriteOutput (bool writeOutput=true)
void	SetWriteOutputEachNewtonIteration (bool writeOutputEachNewtonIteration=true)
void	SetKspAbsoluteTolerance (double kspAbsoluteTolerance)
std::vector< double > &	rGetCurrentSolution ()
std::vector< c_vector< double, DIM > > &	rGetDeformedPosition ()
void	SetCurrentTime (double time)
void	CreateCmguiOutput ()
void	WriteCurrentDeformationGradients (std::string fileName, int counterToAppend)
Protected Member Functions
virtual void	AssembleSystem (bool assembleResidual, bool assembleLinearSystem)=0
void	Initialise ()
void	AllocateMatrixMemory ()
void	ApplyDirichletBoundaryConditions (bool applyToMatrix)
virtual void	FinishAssembleSystem (bool assembleResidual, bool assembleLinearSystem)
double	ComputeResidualAndGetNorm (bool allowException)
double	CalculateResidualNorm ()
void	VectorSum (std::vector< double > &rX, ReplicatableVector &rY, double a, std::vector< double > &rZ)
void	PrintLineSearchResult (double s, double residNorm)
double	TakeNewtonStep ()
double	UpdateSolutionUsingLineSearch (Vec solution)
virtual void	PostNewtonStep (unsigned counter, double normResidual)
void	GetElementCentroidDeformationGradient (Element< DIM, DIM > &rElement, c_matrix< double, DIM, DIM > &rDeformationGradient)
virtual void	ComputeStressAndStressDerivative (AbstractMaterialLaw< DIM > *pMaterialLaw, c_matrix< double, DIM, DIM > &rC, c_matrix< double, DIM, DIM > &rInvC, double pressure, unsigned elementIndex, unsigned currentQuadPointGlobalIndex, c_matrix< double, DIM, DIM > &rT, FourthOrderTensor< DIM, DIM, DIM, DIM > &rDTdE, bool computeDTdE)
Protected Attributes
QuadraticMesh< DIM > &	mrQuadMesh
SolidMechanicsProblemDefinition < DIM > &	mrProblemDefinition
GaussianQuadratureRule< DIM > *	mpQuadratureRule
GaussianQuadratureRule< DIM-1 > *	mpBoundaryQuadratureRule
double	mKspAbsoluteTol
unsigned	mNumDofs
Vec	mResidualVector
Vec	mLinearSystemRhsVector
Mat	mJacobianMatrix
Vec	mDirichletBoundaryConditionsVector
Mat	mPreconditionMatrix
bool	mWriteOutput
std::string	mOutputDirectory
OutputFileHandler *	mpOutputFileHandler
bool	mWriteOutputEachNewtonIteration
std::vector< double >	mCurrentSolution
FourthOrderTensor< DIM, DIM, DIM, DIM >	dTdE
unsigned	mNumNewtonIterations
std::vector< c_vector< double, DIM > >	mDeformedPosition
DeformedBoundaryElement< DIM-1, DIM >	mDeformedBoundaryElement
double	mCurrentTime
CompressibilityType	mCompressibilityType
bool	mCheckedOutwardNormals
Static Protected Attributes
static const size_t	NUM_VERTICES_PER_ELEMENT = DIM+1
static const size_t	NUM_NODES_PER_ELEMENT = (DIM+1)*(DIM+2)/2
static const size_t	NUM_NODES_PER_BOUNDARY_ELEMENT = DIM*(DIM+1)/2
static double	MAX_NEWTON_ABS_TOL = 1e-7
static double	MIN_NEWTON_ABS_TOL = 1e-10
static double	NEWTON_REL_TOL = 1e-4

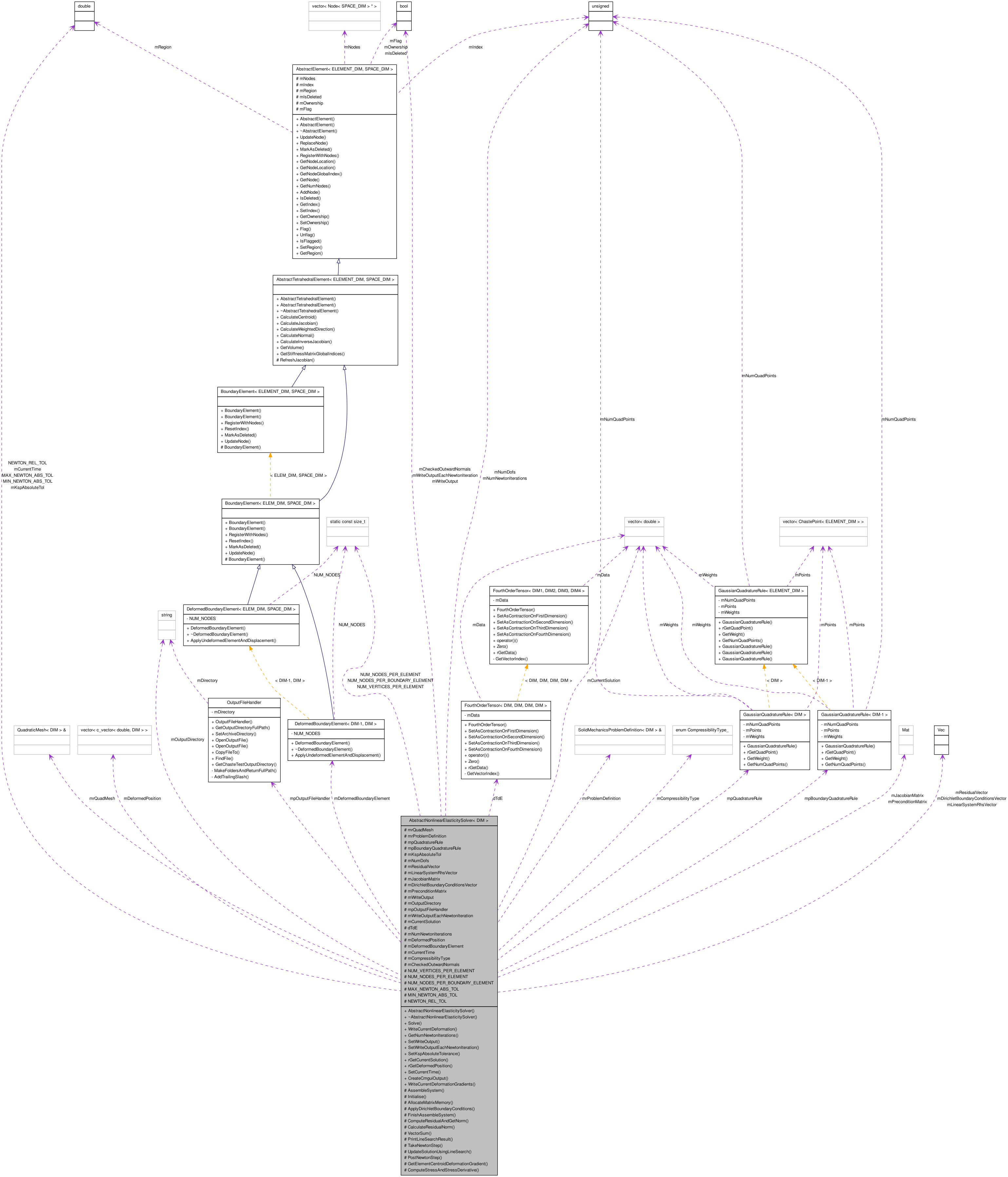
Detailed Description

template<unsigned DIM>
class AbstractNonlinearElasticitySolver< DIM >

Abstract nonlinear elasticity solver.

Definition at line 75 of file AbstractNonlinearElasticitySolver.hpp.

Constructor & Destructor Documentation

template<unsigned DIM>

AbstractNonlinearElasticitySolver< DIM >::AbstractNonlinearElasticitySolver	(	QuadraticMesh< DIM > &	rQuadMesh,
		SolidMechanicsProblemDefinition< DIM > &	rProblemDefinition,
		std::string	outputDirectory,
		CompressibilityType	compressibilityType
	)			`[inline]`

Constructor.

Parameters:

	rQuadMesh	the quadratic mesh
	rProblemDefinition	an object defining in particular the body force and boundary conditions
	outputDirectory	output directory
	compressibilityType	Should be equal to COMPRESSIBLE or INCOMPRESSIBLE (see enumeration defined at top of file) (depending on which concrete class is inheriting from this) and is only used in computing mNumDofs and allocating matrix memory.

Definition at line 1213 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mCompressibilityType, AbstractNonlinearElasticitySolver< DIM >::mNumDofs, AbstractNonlinearElasticitySolver< DIM >::mOutputDirectory, AbstractNonlinearElasticitySolver< DIM >::mpOutputFileHandler, AbstractNonlinearElasticitySolver< DIM >::mrQuadMesh, and AbstractNonlinearElasticitySolver< DIM >::mWriteOutput.

template<unsigned DIM>

AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver ( ) [inline, virtual]

Destructor.

Definition at line 1252 of file AbstractNonlinearElasticitySolver.hpp.

Member Function Documentation

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::AllocateMatrixMemory ( ) [inline, protected]

Allocates memory for the Jacobian and preconditioner matrices (larger number of non-zeros per row than with say linear problems)

We want to allocate different numbers of non-zeros per row, which means PetscTools::SetupMat isn't that useful. We could call

but we would get warnings due to the lack allocation

Definition at line 553 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::Initialise().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions ( bool applyToMatrix ) [inline, protected]

Apply the Dirichlet boundary conditions to the linear system.

This will always apply the Dirichlet boundary conditions to the residual vector (basically, setting a component to the difference between the current value and the correct value).

If the boolean parameter is true, this will apply the boundary conditions to the Jacobian and the linear system RHS vector (which should be equal to the residual on entering this function). In the compressible case the boundary conditions are applied by zeroing both rows and columns of the Jacobian matrix (to maintain) symmetry, which means additional changes are needed for the RHS vector.

Parameters:

applyToMatrix

Whether to apply the boundary conditions to the linear system (as well as the residual).

Definition at line 703 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::FinishAssembleSystem().

template<unsigned DIM>

virtual void AbstractNonlinearElasticitySolver< DIM >::AssembleSystem	(	bool	assembleResidual,
		bool	assembleLinearSystem
	)			`[protected, pure virtual]`

Assemble the residual vector and/or Jacobian matrix (using the current solution stored in mCurrentSolution, output going to mResidualVector and/or mJacobianMatrix).

Must be overridden in concrete derived classes.

Parameters:

	assembleResidual	A bool stating whether to assemble the residual vector.
	assembleLinearSystem	A bool stating whether to assemble the Jacobian matrix and the RHS vector of the linear system (which is based on the residual but could be slightly different due to the way dirichlet boundary conditions are applied to the linear system - see comments in ApplyDirichletBoundaryConditions).

Implemented in CompressibleNonlinearElasticitySolver< DIM >, and IncompressibleNonlinearElasticitySolver< DIM >.

Referenced by AbstractNonlinearElasticitySolver< DIM >::ComputeResidualAndGetNorm(), and AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep().

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::CalculateResidualNorm ( ) [inline, protected]

Calculate |r|_2 / length(r), where r is the current residual vector.

Definition at line 866 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mNumDofs, and AbstractNonlinearElasticitySolver< DIM >::mResidualVector.

Referenced by AbstractNonlinearElasticitySolver< DIM >::ComputeResidualAndGetNorm(), and AbstractNonlinearElasticitySolver< DIM >::UpdateSolutionUsingLineSearch().

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::ComputeResidualAndGetNorm ( bool allowException ) [inline, protected]

Set up the residual vector (using the current solution), and get its scaled norm (Calculate |r|_2 / length(r), where r is residual vector).

Parameters:

allowException

Sometimes the current solution solution will be such that the residual vector cannot be computed, as (say) the material law will throw an exception as the strains are too large. If this bool is set to true, the exception will be caught, and DBL_MAX returned as the residual norm

Definition at line 840 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::AssembleSystem(), and AbstractNonlinearElasticitySolver< DIM >::CalculateResidualNorm().

Referenced by AbstractNonlinearElasticitySolver< DIM >::Solve(), and AbstractNonlinearElasticitySolver< DIM >::UpdateSolutionUsingLineSearch().

template<unsigned DIM>

virtual void AbstractNonlinearElasticitySolver< DIM >::ComputeStressAndStressDerivative	(	AbstractMaterialLaw< DIM > *	pMaterialLaw,
		c_matrix< double, DIM, DIM > &	rC,
		c_matrix< double, DIM, DIM > &	rInvC,
		double	pressure,
		unsigned	elementIndex,
		unsigned	currentQuadPointGlobalIndex,
		c_matrix< double, DIM, DIM > &	rT,
		FourthOrderTensor< DIM, DIM, DIM, DIM > &	rDTdE,
		bool	computeDTdE
	)			`[inline, protected, virtual]`

Simple (one-line function which just calls ComputeStressAndStressDerivative() on the material law given, using C, inv(C), and p as the input and with rT and rDTdE as the output. Overloaded by other assemblers (eg cardiac mechanics) which need to add extra terms to the stress.

Parameters:

	pMaterialLaw	The material law for this element
	rC	The Lagrangian deformation tensor (F^T F)
	rInvC	The inverse of C. Should be computed by the user.
	pressure	The current pressure
	elementIndex	Index of the current element
	currentQuadPointGlobalIndex	The index (assuming an outer loop over elements and an inner loop over quadrature points), of the current quadrature point.
	rT	The stress will be returned in this parameter
	rDTdE	the stress derivative will be returned in this parameter, assuming the final parameter is true
	computeDTdE	A boolean flag saying whether the stress derivative is required or not.

Definition at line 394 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractMaterialLaw< DIM >::ComputeStressAndStressDerivative().

Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), and CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::CreateCmguiOutput ( ) [inline]

Convert the output to Cmgui format (placed in a folder called cmgui in the output directory). Writes the original mesh as solution_0.exnode and the (current) solution as solution_1.exnode.

Definition at line 1476 of file AbstractNonlinearElasticitySolver.hpp.

References EXCEPTION, AbstractNonlinearElasticitySolver< DIM >::mOutputDirectory, AbstractNonlinearElasticitySolver< DIM >::mrQuadMesh, AbstractNonlinearElasticitySolver< DIM >::rGetDeformedPosition(), CmguiDeformedSolutionsWriter< DIM >::WriteCmguiScript(), CmguiDeformedSolutionsWriter< DIM >::WriteDeformationPositions(), and CmguiDeformedSolutionsWriter< DIM >::WriteInitialMesh().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::FinishAssembleSystem	(	bool	assembleResidual,
		bool	assembleLinearSystem
	)			`[inline, protected, virtual]`

To be called at the end of AssembleSystem. Calls (Petsc) assemble methods on the Vecs and Mat, and calls ApplyDirichletBoundaryConditions.

Parameters:

	assembleResidual	see documentation for AssembleSystem
	assembleLinearSystem	see documentation for AssembleSystem

Definition at line 810 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions(), PetscMatTools::Finalise(), PetscVecTools::Finalise(), AbstractNonlinearElasticitySolver< DIM >::mJacobianMatrix, AbstractNonlinearElasticitySolver< DIM >::mLinearSystemRhsVector, AbstractNonlinearElasticitySolver< DIM >::mPreconditionMatrix, AbstractNonlinearElasticitySolver< DIM >::mResidualVector, and PetscMatTools::SwitchWriteMode().

Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), and CompressibleNonlinearElasticitySolver< DIM >::AssembleSystem().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::GetElementCentroidDeformationGradient	(	Element< DIM, DIM > &	rElement,
		c_matrix< double, DIM, DIM > &	rDeformationGradient
	)			`[inline, protected]`

Compute the deformation gradient at the centroid at an element

Parameters:

	rElement	The element
	rDeformationGradient	Reference to a matrix, which will be filled in by this method.

Definition at line 1495 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetIndex(), AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetNodeGlobalIndex(), AbstractNonlinearElasticitySolver< DIM >::mCurrentSolution, AbstractNonlinearElasticitySolver< DIM >::mrQuadMesh, AbstractNonlinearElasticitySolver< DIM >::NUM_NODES_PER_ELEMENT, and ChastePoint< DIM >::rGetLocation().

Referenced by AbstractNonlinearElasticitySolver< DIM >::WriteCurrentDeformationGradients().

template<unsigned DIM>

unsigned AbstractNonlinearElasticitySolver< DIM >::GetNumNewtonIterations ( ) [inline]

Get number of Newton iterations taken in last solve.

Definition at line 1446 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mNumNewtonIterations.

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::Initialise ( void ) [inline, protected]

Initialise the solver.

Definition at line 542 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::AllocateMatrixMemory(), AbstractNonlinearElasticitySolver< DIM >::mCurrentSolution, AbstractNonlinearElasticitySolver< DIM >::mNumDofs, AbstractNonlinearElasticitySolver< DIM >::mpBoundaryQuadratureRule, and AbstractNonlinearElasticitySolver< DIM >::mpQuadratureRule.

Referenced by CompressibleNonlinearElasticitySolver< DIM >::CompressibleNonlinearElasticitySolver(), and IncompressibleNonlinearElasticitySolver< DIM >::IncompressibleNonlinearElasticitySolver().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::PostNewtonStep	(	unsigned	counter,
		double	normResidual
	)			`[inline, protected, virtual]`

This function may be overloaded by subclasses. It is called after each Newton iteration.

Parameters:

	counter	current newton iteration number
	normResidual	norm of the residual

Definition at line 1208 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::PrintLineSearchResult	(	double	s,
		double	residNorm
	)			`[inline, protected]`

Print to std::cout the residual norm for this s, ie ||f(x+su)|| where f is the residual vector, x the current solution and u the update vector.

Parameters:

	s	s
	residNorm	residual norm.

Definition at line 1107 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::UpdateSolutionUsingLineSearch().

template<unsigned DIM>

std::vector<double>& AbstractNonlinearElasticitySolver< DIM >::rGetCurrentSolution ( ) [inline]

Get the current solution vector (advanced use only - for getting the deformed position use rGetDeformedPosition().

Definition at line 494 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mCurrentSolution.

template<unsigned DIM>

std::vector< c_vector< double, DIM > > & AbstractNonlinearElasticitySolver< DIM >::rGetDeformedPosition ( ) [inline]

Get the deformed position. Note returnvalue[i](j) = x_j for node i.

Definition at line 1462 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mCurrentSolution, AbstractNonlinearElasticitySolver< DIM >::mDeformedPosition, and AbstractNonlinearElasticitySolver< DIM >::mrQuadMesh.

Referenced by AbstractNonlinearElasticitySolver< DIM >::CreateCmguiOutput(), and AbstractNonlinearElasticitySolver< DIM >::WriteCurrentDeformation().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::SetCurrentTime ( double time ) [inline]

This solver is for static problems, however the body force or surface tractions could be a function of time. This method is for setting the time.

Parameters:

time

current time

Definition at line 511 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mCurrentTime.

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::SetKspAbsoluteTolerance ( double kspAbsoluteTolerance ) [inline]

Set the absolute tolerance to be used when solving the linear system. If this is not called a relative tolerance is used.

Parameters:

kspAbsoluteTolerance

the tolerance

Definition at line 484 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mKspAbsoluteTol.

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::SetWriteOutput ( bool writeOutput = true ) [inline]

Set whether to write any output.

Parameters:

writeOutput

(defaults to true)

Definition at line 1452 of file AbstractNonlinearElasticitySolver.hpp.

References EXCEPTION, AbstractNonlinearElasticitySolver< DIM >::mOutputDirectory, and AbstractNonlinearElasticitySolver< DIM >::mWriteOutput.

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::SetWriteOutputEachNewtonIteration ( bool writeOutputEachNewtonIteration = true ) [inline]

By default only the original and converged solutions are written. Call this by get node positions written after every Newton step (mostly for debugging).

Parameters:

writeOutputEachNewtonIteration

whether to write each iteration

Definition at line 473 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mWriteOutputEachNewtonIteration.

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::Solve	(	double	tol = `-1.0`,
		unsigned	maxNumNewtonIterations = `INT_MAX`,
		bool	quitIfNoConvergence = `true`
	)			`[inline]`

Solve the problem.

Parameters:

	tol	tolerance used in Newton solve (defaults to -1.0)
	maxNumNewtonIterations	(defaults to INT_MAX)
	quitIfNoConvergence	(defaults to true)

Definition at line 1278 of file AbstractNonlinearElasticitySolver.hpp.

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep ( ) [inline, protected]

Take one newton step, by solving the linear system -Ju=f, (J the jacobian, f the residual, u the update), and picking s such that a_new = a_old + su (a the current solution) such |f(a)| is the smallest.

Returns:: The current norm of the residual after the newton step.

Todo:: : #1913 this only works in sequential

Definition at line 889 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::UpdateSolutionUsingLineSearch ( Vec solution ) [inline, protected]

Using the update vector (of Newton's method), choose s such that ||f(x+su)|| is most decreased, where f is the residual vector, x the current solution (mCurrentSolution) and u the update vector. This checks s=1 first (most likely to be the current solution, then 0.9, 0.8.. until ||f|| starts increasing.

Parameters:

solution

The solution of the linear solve in newton's method, ie the update vector u.

Definition at line 1115 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::CalculateResidualNorm(), AbstractNonlinearElasticitySolver< DIM >::ComputeResidualAndGetNorm(), AbstractNonlinearElasticitySolver< DIM >::mCurrentSolution, AbstractNonlinearElasticitySolver< DIM >::PrintLineSearchResult(), and AbstractNonlinearElasticitySolver< DIM >::VectorSum().

Referenced by AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::VectorSum	(	std::vector< double > &	rX,
		ReplicatableVector &	rY,
		double	a,
		std::vector< double > &	rZ
	)			`[inline, protected]`

Simple helper function, computes Z = X + aY, where X and Z are std::vectors and Y a ReplicatableVector.

Parameters:

	rX	X
	rY	Y (replicatable vector)
	a	a
	rZ	Z the returned vector

Definition at line 874 of file AbstractNonlinearElasticitySolver.hpp.

References ReplicatableVector::GetSize().

Referenced by AbstractNonlinearElasticitySolver< DIM >::UpdateSolutionUsingLineSearch().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::WriteCurrentDeformation	(	std::string	fileName,
		int	counterToAppend = `-1`
	)			`[inline]`

Write the current deformation of the nodes.

Parameters:

	fileName	(stem)
	counterToAppend	append a counter to the file name

For example: WriteCurrentDeformation("solution") --> file called "solution.nodes" WriteCurrentDeformation("solution",3) --> file called "solution_3.nodes"

Definition at line 1378 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::mpOutputFileHandler, AbstractNonlinearElasticitySolver< DIM >::mWriteOutput, OutputFileHandler::OpenOutputFile(), and AbstractNonlinearElasticitySolver< DIM >::rGetDeformedPosition().

Referenced by AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

void AbstractNonlinearElasticitySolver< DIM >::WriteCurrentDeformationGradients	(	std::string	fileName,
		int	counterToAppend
	)			`[inline]`

Write the deformation gradients for each element (evaluated at the centroids of each element) Each line of the output file corresponds to one element: the DIM*DIM matrix will be written as one line, using the ordering: F00 F01 F02 F10 F11 F12 F20 F21 F22.

Parameters:

	fileName	The file name stem
	counterToAppend	Number to append in the filename.

The final file is [fileName]_[counterToAppend].strain

Definition at line 1409 of file AbstractNonlinearElasticitySolver.hpp.

References AbstractNonlinearElasticitySolver< DIM >::GetElementCentroidDeformationGradient(), AbstractNonlinearElasticitySolver< DIM >::mpOutputFileHandler, AbstractNonlinearElasticitySolver< DIM >::mrQuadMesh, AbstractNonlinearElasticitySolver< DIM >::mWriteOutput, and OutputFileHandler::OpenOutputFile().

Member Data Documentation

template<unsigned DIM>

FourthOrderTensor<DIM,DIM,DIM,DIM> AbstractNonlinearElasticitySolver< DIM >::dTdE [protected]

Storage space for a 4th order tensor used in assembling the Jacobian (to avoid repeated memory allocation).

Definition at line 216 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), and CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement().

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::MAX_NEWTON_ABS_TOL = 1e-7 [inline, static, protected]

Maximum absolute tolerance for Newton solve. The Newton solver uses the absolute tolerance corresponding to the specified relative tolerance, but has a max and min allowable absolute tolerance. (ie: if max_abs = 1e-7, min_abs = 1e-10, rel=1e-4: then if the norm of the initial_residual (=a) is 1e-2, it will solve with tolerance 1e-7; if a=1e-5, it will solve with tolerance 1e-9; a=1e-9, it will solve with tolerance 1e-10.

Definition at line 95 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

bool AbstractNonlinearElasticitySolver< DIM >::mCheckedOutwardNormals [protected]

Whether the boundary elements of the mesh have been checked for whether the ordering if such that the normals are outward-facing

Definition at line 249 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

CompressibilityType AbstractNonlinearElasticitySolver< DIM >::mCompressibilityType [protected]

This is equal to either COMPRESSIBLE or INCOMPRESSIBLE (see enumeration defined at top of file) and is only used in computing mNumDofs and allocating matrix memory.

Definition at line 244 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AbstractNonlinearElasticitySolver(), AbstractNonlinearElasticitySolver< DIM >::AllocateMatrixMemory(), AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions(), AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

std::vector<double> AbstractNonlinearElasticitySolver< DIM >::mCurrentSolution [protected]

The current solution, in the form (assuming 2d): Incompressible problem: [u1 v1 u2 v2 ... uN vN p1 p2 .. pM] Compressible problem: [u1 v1 u2 v2 ... uN vN] where there are N total nodes and M vertices.

Definition at line 211 of file AbstractNonlinearElasticitySolver.hpp.

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::mCurrentTime [protected]

This solver is for static problems, however the body force or surface tractions could be a function of time. The user should call SetCurrentTime() if this is the case.

Definition at line 238 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), and AbstractNonlinearElasticitySolver< DIM >::SetCurrentTime().

template<unsigned DIM>

DeformedBoundaryElement<DIM-1,DIM> AbstractNonlinearElasticitySolver< DIM >::mDeformedBoundaryElement [protected]

For a particular type of boundary condition - prescribed pressures acting on the deformed surface, we need to do surface integrals over the deformed surface. This object is a helper object for this, it takes in a base boundary element and a set of displacements, and sets up the deformed boundary element. Only used if mProblemDefinition.GetTractionBoundaryConditionType()==PRESSURE_ON_DEFORMED)

Definition at line 231 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), and CompressibleNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement().

template<unsigned DIM>

std::vector<c_vector<double,DIM> > AbstractNonlinearElasticitySolver< DIM >::mDeformedPosition [protected]

Deformed position: mDeformedPosition[i](j) = x_j for node i.

Definition at line 222 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::rGetDeformedPosition().

template<unsigned DIM>

Vec AbstractNonlinearElasticitySolver< DIM >::mDirichletBoundaryConditionsVector [protected]

Helper vector (see ApplyDirichletBoundaryConditions code).

Definition at line 167 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AllocateMatrixMemory(), AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::MIN_NEWTON_ABS_TOL = 1e-10 [inline, static, protected]

Minimum absolute tolerance for Newton solve. See documentation for MAX_NEWTON_ABS_TOL.

Definition at line 98 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

Mat AbstractNonlinearElasticitySolver< DIM >::mJacobianMatrix [protected]

Jacobian matrix of the nonlinear system, LHS matrix for the linear system.

Definition at line 162 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AllocateMatrixMemory(), AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), CompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), AbstractNonlinearElasticitySolver< DIM >::FinishAssembleSystem(), AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::mKspAbsoluteTol [protected]

Absolute tolerance for linear systems. Can be set by calling SetKspAbsoluteTolerances(), but default to -1, in which case a relative tolerance is used.

Definition at line 126 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::SetKspAbsoluteTolerance(), and AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep().

template<unsigned DIM>

Vec AbstractNonlinearElasticitySolver< DIM >::mLinearSystemRhsVector [protected]

The RHS side in the linear system that is solved each Newton iteration. Since Newton's method is Ju = f, where J is the Jacobian, u the (negative of the) update and f the residual, it might seem necessary to store this as well as the residual. However, when applying Dirichlet boundary conditions in the compressible case, we alter the rows of the matrix, but also alter the columns in order to maintain symmetry. This requires making further changes to the right-hand vector, meaning that it no longer properly represents the residual. Hence, we have to use two vectors.

Overall, this can be represents as

compute residual f
compute Jacobian J
apply BCs to f.
alter the linear system from Ju=f to (J*)u=f* which enforces the dirichlet boundary conditions but enforces them symmetrically.

mLinearSystemRhsVector represents f*.

Definition at line 157 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AllocateMatrixMemory(), AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions(), AbstractNonlinearElasticitySolver< DIM >::FinishAssembleSystem(), AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

unsigned AbstractNonlinearElasticitySolver< DIM >::mNumDofs [protected]

Number of degrees of freedom (equal to, in the incompressible case: DIM*N + M if quadratic-linear bases are used, where there are N total nodes and M vertices; or DIM*N in the compressible case).

Definition at line 133 of file AbstractNonlinearElasticitySolver.hpp.

template<unsigned DIM>

unsigned AbstractNonlinearElasticitySolver< DIM >::mNumNewtonIterations [protected]

Number of Newton iterations taken in last solve.

Definition at line 219 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::GetNumNewtonIterations(), and AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

std::string AbstractNonlinearElasticitySolver< DIM >::mOutputDirectory [protected]

Where to write output, relative to CHASTE_TESTOUTPUT.

Definition at line 193 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AbstractNonlinearElasticitySolver(), AbstractNonlinearElasticitySolver< DIM >::CreateCmguiOutput(), and AbstractNonlinearElasticitySolver< DIM >::SetWriteOutput().

template<unsigned DIM>

GaussianQuadratureRule<DIM-1>* AbstractNonlinearElasticitySolver< DIM >::mpBoundaryQuadratureRule [protected]

Boundary Gaussian quadrature rule.

Definition at line 119 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), AbstractNonlinearElasticitySolver< DIM >::Initialise(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

OutputFileHandler* AbstractNonlinearElasticitySolver< DIM >::mpOutputFileHandler [protected]

Output file handler.

Definition at line 196 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AbstractNonlinearElasticitySolver(), AbstractNonlinearElasticitySolver< DIM >::WriteCurrentDeformation(), AbstractNonlinearElasticitySolver< DIM >::WriteCurrentDeformationGradients(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

GaussianQuadratureRule<DIM>* AbstractNonlinearElasticitySolver< DIM >::mpQuadratureRule [protected]

Gaussian quadrature rule.

Definition at line 116 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), AbstractNonlinearElasticitySolver< DIM >::Initialise(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

Mat AbstractNonlinearElasticitySolver< DIM >::mPreconditionMatrix [protected]

Precondition matrix for the linear system.

In the incompressible case: the preconditioner is the petsc LU factorisation of

Jp = [A B] in displacement-pressure block form, [C M]

where the A, B and C are the matrices in the normal jacobian, i.e.

J = [A B] [C 0]

and M is the MASS MATRIX (ie integral phi_i phi_j dV, where phi_i are the pressure basis functions).

Definition at line 187 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AllocateMatrixMemory(), AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), CompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), AbstractNonlinearElasticitySolver< DIM >::FinishAssembleSystem(), AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

Vec AbstractNonlinearElasticitySolver< DIM >::mResidualVector [protected]

Residual vector for the full nonlinear system, also the RHS vector in the linear system used to solve the nonlinear problem using Newton's method.

Definition at line 139 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AllocateMatrixMemory(), AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), CompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), AbstractNonlinearElasticitySolver< DIM >::CalculateResidualNorm(), AbstractNonlinearElasticitySolver< DIM >::FinishAssembleSystem(), AbstractNonlinearElasticitySolver< DIM >::TakeNewtonStep(), and AbstractNonlinearElasticitySolver< DIM >::~AbstractNonlinearElasticitySolver().

template<unsigned DIM>

SolidMechanicsProblemDefinition<DIM>& AbstractNonlinearElasticitySolver< DIM >::mrProblemDefinition [protected]

This class contains all the information about the problem (except the material law): body force, surface tractions, fixed nodes, density

Definition at line 113 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::ApplyDirichletBoundaryConditions(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), CompressibleNonlinearElasticitySolver< DIM >::AssembleSystem(), IncompressibleNonlinearElasticitySolver< DIM >::FormInitialGuess(), and AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

QuadraticMesh<DIM>& AbstractNonlinearElasticitySolver< DIM >::mrQuadMesh [protected]

The mesh to be solved on. Requires 6 nodes per triangle (or 10 per tetrahedron) as quadratic bases are used.

Definition at line 107 of file AbstractNonlinearElasticitySolver.hpp.

template<unsigned DIM>

bool AbstractNonlinearElasticitySolver< DIM >::mWriteOutput [protected]

Whether to write any output.

Definition at line 190 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::AbstractNonlinearElasticitySolver(), AbstractNonlinearElasticitySolver< DIM >::SetWriteOutput(), AbstractNonlinearElasticitySolver< DIM >::WriteCurrentDeformation(), and AbstractNonlinearElasticitySolver< DIM >::WriteCurrentDeformationGradients().

template<unsigned DIM>

bool AbstractNonlinearElasticitySolver< DIM >::mWriteOutputEachNewtonIteration [protected]

By default only the initial and final solutions are written. However, we may want to write the solutions after every Newton iteration, in which case the following should be set to true.

Definition at line 203 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::SetWriteOutputEachNewtonIteration(), and AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

double AbstractNonlinearElasticitySolver< DIM >::NEWTON_REL_TOL = 1e-4 [inline, static, protected]

Relative tolerance for Newton solve. See documentation for MAX_NEWTON_ABS_TOL.

Definition at line 101 of file AbstractNonlinearElasticitySolver.hpp.

Referenced by AbstractNonlinearElasticitySolver< DIM >::Solve().

template<unsigned DIM>

const size_t AbstractNonlinearElasticitySolver< DIM >::NUM_NODES_PER_BOUNDARY_ELEMENT = DIM*(DIM+1)/2 [static, protected]

Number of nodes per boundary element.

Reimplemented in CompressibleNonlinearElasticitySolver< DIM >, and IncompressibleNonlinearElasticitySolver< DIM >.

Definition at line 86 of file AbstractNonlinearElasticitySolver.hpp.