CompressibleMooneyRivlinMaterialLaw< DIM > Class Template Reference

#include <CompressibleMooneyRivlinMaterialLaw.hpp>

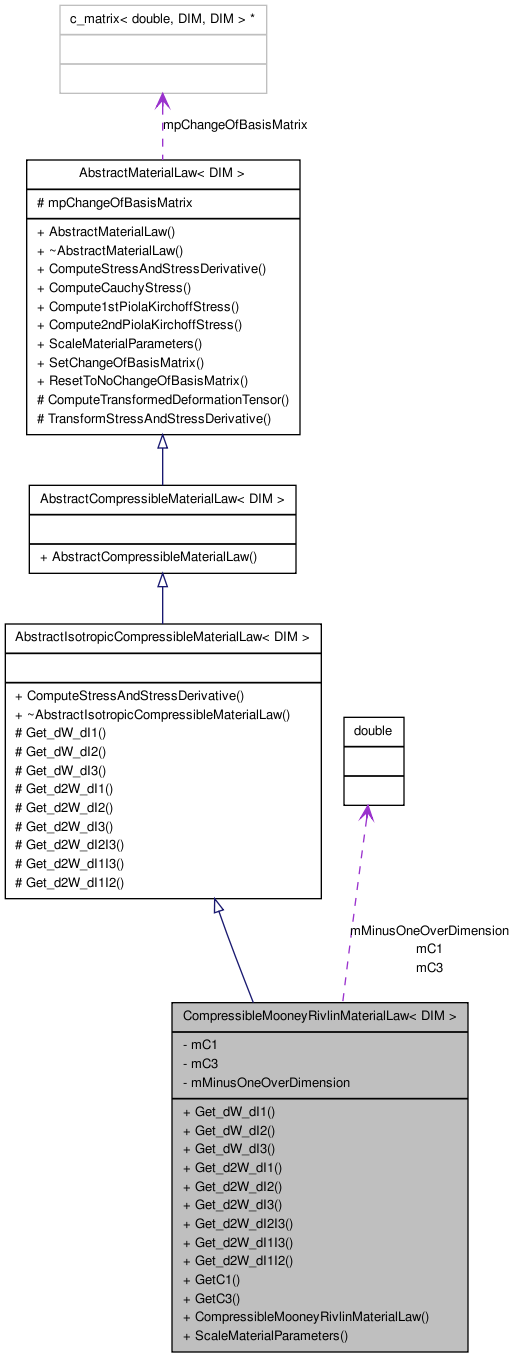
Inherits AbstractIsotropicCompressibleMaterialLaw< DIM >.

Collaboration diagram for CompressibleMooneyRivlinMaterialLaw< DIM >:
Collaboration graph
[legend]

List of all members.

Public Member Functions

double Get_dW_dI1 (double I1, double I2, double I3)
double Get_dW_dI2 (double I1, double I2, double I3)
double Get_dW_dI3 (double I1, double I2, double I3)
double Get_d2W_dI1 (double I1, double I2, double I3)
double Get_d2W_dI2 (double I1, double I2, double I3)
double Get_d2W_dI3 (double I1, double I2, double I3)
double Get_d2W_dI2I3 (double I1, double I2, double I3)
double Get_d2W_dI1I3 (double I1, double I2, double I3)
double Get_d2W_dI1I2 (double I1, double I2, double I3)
double GetC1 ()
double GetC3 ()
 CompressibleMooneyRivlinMaterialLaw (double c1, double c3)
void ScaleMaterialParameters (double scaleFactor)

Private Attributes

double mC1
double mC3

Static Private Attributes

static const double mMinusOneOverDimension = -1.0/DIM

Detailed Description

template<unsigned DIM>
class CompressibleMooneyRivlinMaterialLaw< DIM >

CompressibleMooneyRivlinMaterialLaw

A Mooney-Rivlin isotropic compressible hyperelastic material law for finite elasticity

The law is given by a strain energy function W(I1,I2,I3) = c1 ( dev(I1)-3 ) + c3(J-1)^2

where (assuming Ii are the principal invariants of C, the Lagrangian deformation tensor, I1=trace(C), I2=0.5(trace(C)^2-trace(C^2)), I3=det(C)): J = det(F) = sqrt(I3) dev(I1) = I1 * J^(-2/DIM) is the first invariant of the deviatoric part of C

Note T(E=0) = 0 regardless of choice of c1, c3.

NOTE: this is really just a NEO-HOOKEAN law at present - the c2 (dev(I2)-3) term hasn't been added yet...

Definition at line 59 of file CompressibleMooneyRivlinMaterialLaw.hpp.

Constructor & Destructor Documentation

template<unsigned DIM>
CompressibleMooneyRivlinMaterialLaw< DIM >::CompressibleMooneyRivlinMaterialLaw ( double  c1,
double  c3 
) [inline]

Constructor, taking in parameters c1 and c3.

Parameters:
c1 parameter c1
c3 parameter c3

Definition at line 209 of file CompressibleMooneyRivlinMaterialLaw.hpp.

References CompressibleMooneyRivlinMaterialLaw< DIM >::mC1, and CompressibleMooneyRivlinMaterialLaw< DIM >::mC3.

Member Function Documentation

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI1 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the second derivative d^2W/dI1^2.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 118 of file CompressibleMooneyRivlinMaterialLaw.hpp.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI1I2 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the second derivative d^2W/dI1dI2.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 185 of file CompressibleMooneyRivlinMaterialLaw.hpp.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI1I3 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the second derivative d^2W/dI1dI3.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 172 of file CompressibleMooneyRivlinMaterialLaw.hpp.

References CompressibleMooneyRivlinMaterialLaw< DIM >::mC1, and CompressibleMooneyRivlinMaterialLaw< DIM >::mMinusOneOverDimension.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI2 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the second derivative d^2W/dI2^2.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 131 of file CompressibleMooneyRivlinMaterialLaw.hpp.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI2I3 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the second derivative d^2W/dI2dI3.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 159 of file CompressibleMooneyRivlinMaterialLaw.hpp.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI3 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the second derivative d^2W/dI3^2.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 144 of file CompressibleMooneyRivlinMaterialLaw.hpp.

References CompressibleMooneyRivlinMaterialLaw< DIM >::mC1, CompressibleMooneyRivlinMaterialLaw< DIM >::mC3, and CompressibleMooneyRivlinMaterialLaw< DIM >::mMinusOneOverDimension.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_dW_dI1 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the first derivative dW/dI1.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 81 of file CompressibleMooneyRivlinMaterialLaw.hpp.

References CompressibleMooneyRivlinMaterialLaw< DIM >::mC1, and CompressibleMooneyRivlinMaterialLaw< DIM >::mMinusOneOverDimension.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_dW_dI2 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the first derivative dW/dI2.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 93 of file CompressibleMooneyRivlinMaterialLaw.hpp.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::Get_dW_dI3 ( double  I1,
double  I2,
double  I3 
) [inline, virtual]

Get the first derivative dW/dI3.

Parameters:
I1 first principal invariant of C
I2 second principal invariant of C
I3 third principal invariant of C

Implements AbstractIsotropicCompressibleMaterialLaw< DIM >.

Definition at line 105 of file CompressibleMooneyRivlinMaterialLaw.hpp.

References CompressibleMooneyRivlinMaterialLaw< DIM >::mC1, CompressibleMooneyRivlinMaterialLaw< DIM >::mC3, and CompressibleMooneyRivlinMaterialLaw< DIM >::mMinusOneOverDimension.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::GetC1 (  )  [inline]

Get method for mC1.

Definition at line 192 of file CompressibleMooneyRivlinMaterialLaw.hpp.

References CompressibleMooneyRivlinMaterialLaw< DIM >::mC1.

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::GetC3 (  )  [inline]

Get method for mC3.

Definition at line 198 of file CompressibleMooneyRivlinMaterialLaw.hpp.

References CompressibleMooneyRivlinMaterialLaw< DIM >::mC3.

template<unsigned DIM>
void CompressibleMooneyRivlinMaterialLaw< DIM >::ScaleMaterialParameters ( double  scaleFactor  )  [inline, virtual]

Scale the dimensional material parameters.

Parameters:
scaleFactor 

Reimplemented from AbstractMaterialLaw< DIM >.

Definition at line 221 of file CompressibleMooneyRivlinMaterialLaw.hpp.

References CompressibleMooneyRivlinMaterialLaw< DIM >::mC1, and CompressibleMooneyRivlinMaterialLaw< DIM >::mC3.

Member Data Documentation

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::mC1 [private]

Parameter c1.

Definition at line 64 of file CompressibleMooneyRivlinMaterialLaw.hpp.

Referenced by CompressibleMooneyRivlinMaterialLaw< DIM >::CompressibleMooneyRivlinMaterialLaw(), CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI1I3(), CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI3(), CompressibleMooneyRivlinMaterialLaw< DIM >::Get_dW_dI1(), CompressibleMooneyRivlinMaterialLaw< DIM >::Get_dW_dI3(), CompressibleMooneyRivlinMaterialLaw< DIM >::GetC1(), and CompressibleMooneyRivlinMaterialLaw< DIM >::ScaleMaterialParameters().

template<unsigned DIM>
double CompressibleMooneyRivlinMaterialLaw< DIM >::mC3 [private]

Parameter c3

Definition at line 67 of file CompressibleMooneyRivlinMaterialLaw.hpp.

Referenced by CompressibleMooneyRivlinMaterialLaw< DIM >::CompressibleMooneyRivlinMaterialLaw(), CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI3(), CompressibleMooneyRivlinMaterialLaw< DIM >::Get_dW_dI3(), CompressibleMooneyRivlinMaterialLaw< DIM >::GetC3(), and CompressibleMooneyRivlinMaterialLaw< DIM >::ScaleMaterialParameters().

template<unsigned DIM>
const double CompressibleMooneyRivlinMaterialLaw< DIM >::mMinusOneOverDimension = -1.0/DIM [static, private]

-1.0/DIM

Definition at line 70 of file CompressibleMooneyRivlinMaterialLaw.hpp.

Referenced by CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI1I3(), CompressibleMooneyRivlinMaterialLaw< DIM >::Get_d2W_dI3(), CompressibleMooneyRivlinMaterialLaw< DIM >::Get_dW_dI1(), and CompressibleMooneyRivlinMaterialLaw< DIM >::Get_dW_dI3().

The documentation for this class was generated from the following file:
Generated on Thu Dec 22 13:03:33 2011 for Chaste by  doxygen 1.6.3