ExtendedBidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM > Class Template Reference
#include <ExtendedBidomainNeumannSurfaceTermAssembler.hpp>
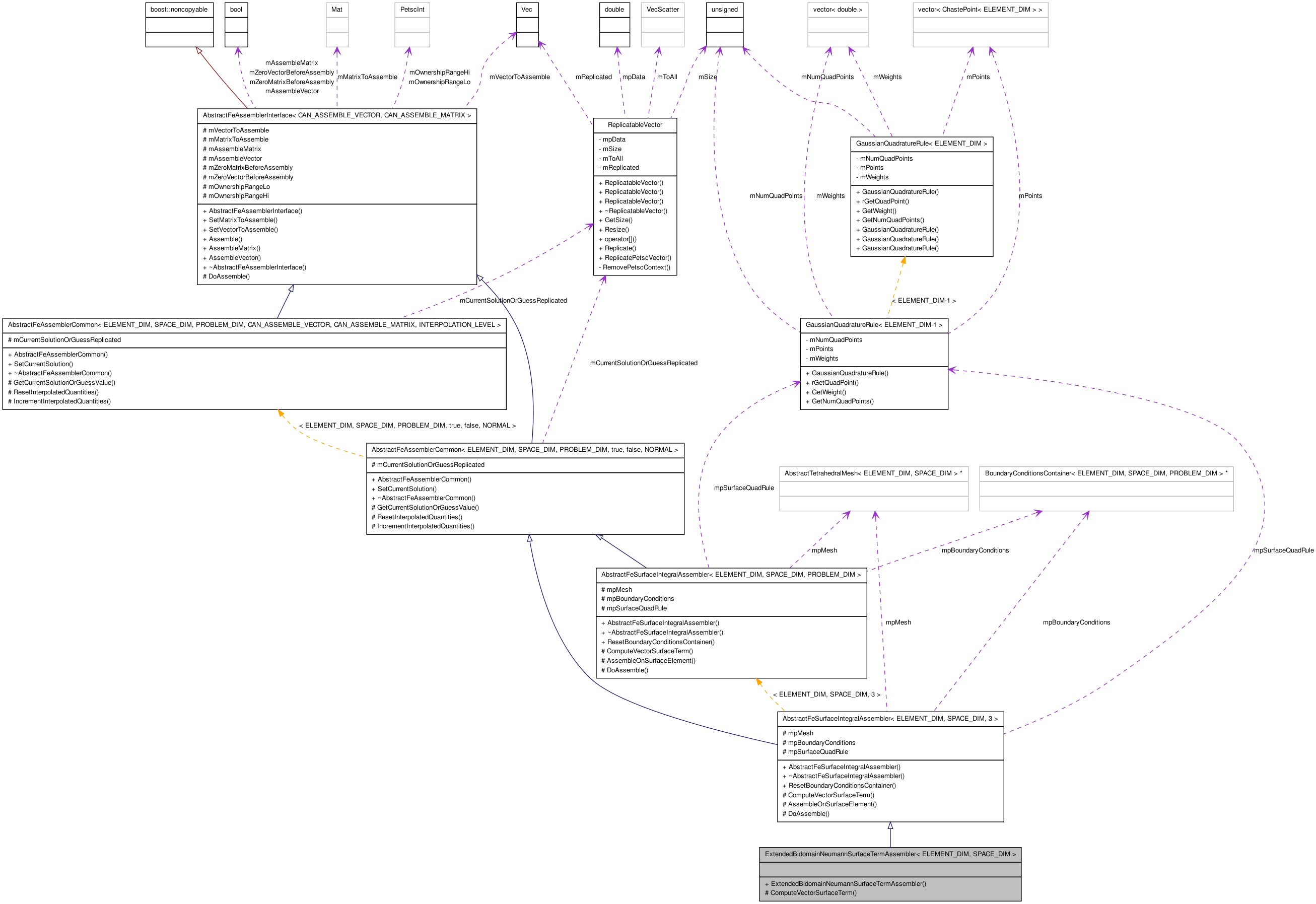
Inherits AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, 3 >.
Public Member Functions | |
| ExtendedBidomainNeumannSurfaceTermAssembler (AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *pMesh, BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 3 > *pBoundaryConditions, unsigned numQuadPoints=2) | |
Protected Member Functions | |
| virtual c_vector< double, 3 *ELEMENT_DIM > | ComputeVectorSurfaceTerm (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, ELEMENT_DIM > &rPhi, ChastePoint< SPACE_DIM > &rX) |
Detailed Description
template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
class ExtendedBidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM >
Assembler which sets up the surface integral integrals for the extended bidomain equations, assuming that the boundary conditions are written: div(sigma_i_1 grad phi_i_1) . n = g1, div(sigma_i_2 grad phi_i_2) . n = g2 and div(sigma_e grad phi_e) dot n = g3.
Definition at line 43 of file ExtendedBidomainNeumannSurfaceTermAssembler.hpp.
Constructor & Destructor Documentation
| ExtendedBidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM >::ExtendedBidomainNeumannSurfaceTermAssembler | ( | AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > * | pMesh, | |
| BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 3 > * | pBoundaryConditions, | |||
| unsigned | numQuadPoints = 2 | |||
| ) | [inline] |
Constructor
- Parameters:
-
pMesh The mesh pBoundaryConditions The boundary conditions container numQuadPoints Number of quad points (per dimension) to use
Definition at line 76 of file ExtendedBidomainNeumannSurfaceTermAssembler.hpp.
Member Function Documentation
| c_vector< double, 3 *ELEMENT_DIM > ExtendedBidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM >::ComputeVectorSurfaceTerm | ( | const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > & | rSurfaceElement, | |
| c_vector< double, ELEMENT_DIM > & | rPhi, | |||
| ChastePoint< SPACE_DIM > & | rX | |||
| ) | [inline, protected, virtual] |
This method is called by AssembleOnSurfaceElement() and tells the assembler what to add to the element stiffness matrix arising from surface element contributions.
NOTE: this method has to be implemented but shouldn't ever be called - because all bidomain problems (currently) just have zero Neumann boundary conditions and the AbstractLinearAssmebler::AssembleSystem() method will realise this and not loop over surface elements.
- Parameters:
-
rSurfaceElement the element which is being considered. rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases rX The point in space
Reimplemented from AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, 3 >.
Definition at line 87 of file ExtendedBidomainNeumannSurfaceTermAssembler.hpp.
References AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, 3 >::mpBoundaryConditions.
The documentation for this class was generated from the following file:
- heart/src/solver/electrics/extended_bidomain/ExtendedBidomainNeumannSurfaceTermAssembler.hpp
 1.6.3
1.6.3