NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > Class Template Reference
#include <NaturalNeumannSurfaceTermAssembler.hpp>
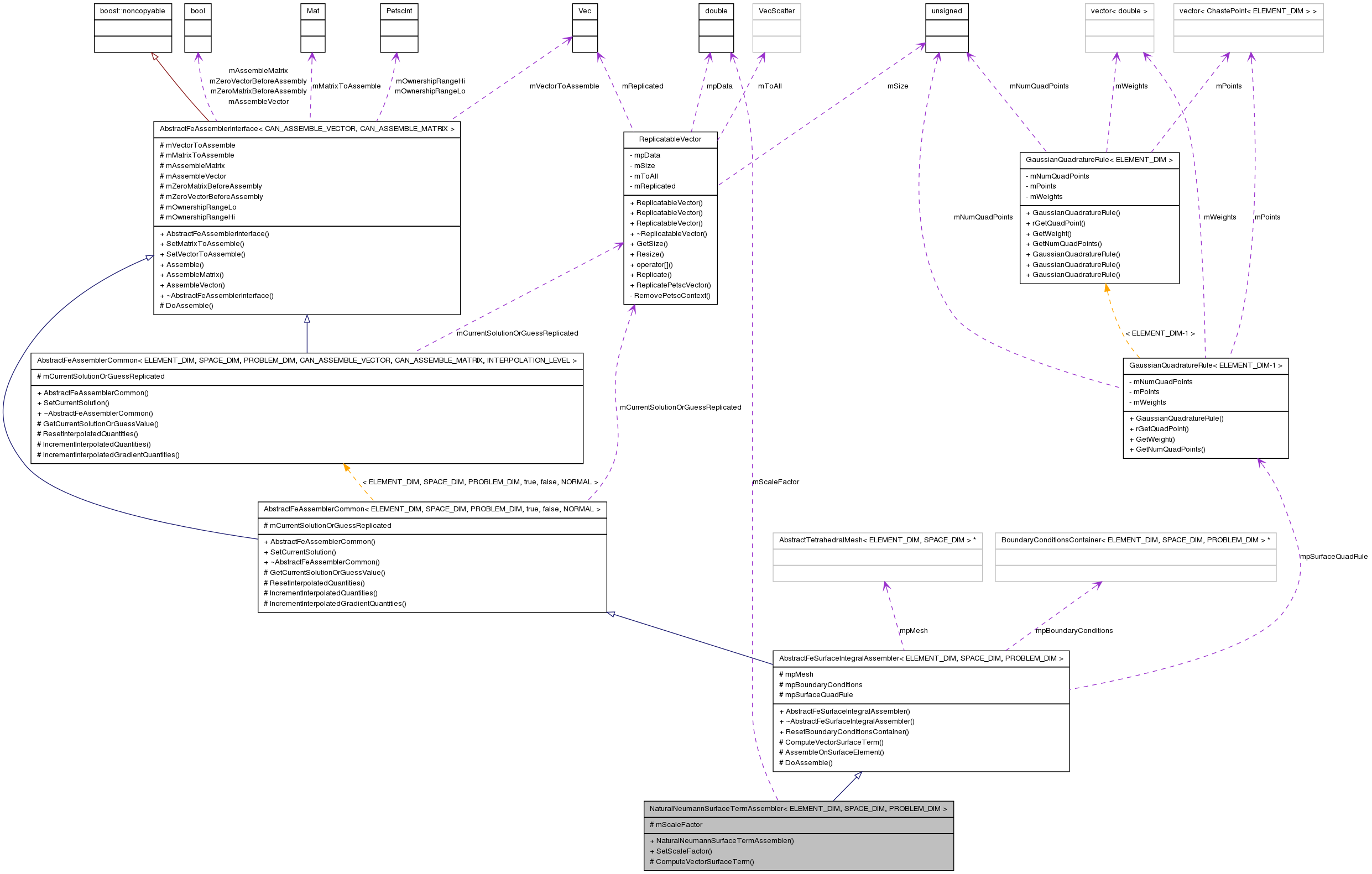
Inherits AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >.
Public Member Functions | |
| NaturalNeumannSurfaceTermAssembler (AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *pMesh, BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > *pBoundaryConditions) | |
| void | SetScaleFactor (double scaleFactor) |
Protected Member Functions | |
| virtual c_vector< double, PROBLEM_DIM *ELEMENT_DIM > | ComputeVectorSurfaceTerm (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, ELEMENT_DIM > &rPhi, ChastePoint< SPACE_DIM > &rX) |
Protected Attributes | |
| double | mScaleFactor |
Detailed Description
template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>
class NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >
An assembler for assembling surface element contributions to a vector coming from Neumann boundary conditions, assuming the prescribed BCs are NATURAL boundary conditions.
Examples of natural BCs: u_t = u_{xx} +f ---> natural BCs are specification of (u_x . n) = g u_t = Laplacian(u) +f ---> natural BCs are specification of (grad(u) . n) = g u_t = Div (D grad(u)) ---> natural BCs are specification of ( (D grad(u)) . n) = g 0 = Div (D grad(u)) ---> natural BCs are specification of ( (D grad(u)) . n) = g 0 = Div (D1 grad(u1)) + Div (D2 grad(u2)) (one equation of a 2-unknown problem) ---> natural BCs are specification of ( (D1 grad(u1)) . n + (D2 grad(u2)) . n) = g1
In all cases, when in weak form, the surface integral is integral(gv dS), where v is the test function (or integral_over_Gamma(g1*v1+g2*v2 dS) in the 2-unknown case).
The contribution of the finite element vector is therefore always: the STRIPED version of the following BLOCK vector: [c1 c2 .. cP], where P = PROBLEM_DIM, each c_i is of dimension N (number of nodes/bases), and c1 has entries `integral_over_Gamma (g1*phi_i dS)`, etc.
Definition at line 62 of file NaturalNeumannSurfaceTermAssembler.hpp.
Constructor & Destructor Documentation
| NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::NaturalNeumannSurfaceTermAssembler | ( | AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > * | pMesh, | |
| BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > * | pBoundaryConditions | |||
| ) | [inline] |
Constructor
- Parameters:
-
pMesh The mesh pBoundaryConditions The boundary conditions container
Definition at line 95 of file NaturalNeumannSurfaceTermAssembler.hpp.
Member Function Documentation
| c_vector< double, PROBLEM_DIM *ELEMENT_DIM > NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ComputeVectorSurfaceTerm | ( | const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > & | rSurfaceElement, | |
| c_vector< double, ELEMENT_DIM > & | rPhi, | |||
| ChastePoint< SPACE_DIM > & | rX | |||
| ) | [inline, protected, virtual] |
- Returns:
- the vector to be added to full vector for a given Gauss point in BoundaryElement, ie, essentially the INTEGRAND in the boundary integral part of the definition of the vector. The arguments are the bases, x and current solution computed at the Gauss point.
Returns the integrand corresponding to natural Neumann BCs being specified.
- Parameters:
-
rSurfaceElement the element which is being considered. rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases rX The point in space
Reimplemented from AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >.
Definition at line 115 of file NaturalNeumannSurfaceTermAssembler.hpp.
References AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpBoundaryConditions, and NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mScaleFactor.
| void NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::SetScaleFactor | ( | double | scaleFactor | ) | [inline] |
Set a scale factor to multiply the contribution to the vector that is assembled by this class
- Parameters:
-
scaleFactor
Definition at line 106 of file NaturalNeumannSurfaceTermAssembler.hpp.
Member Data Documentation
double NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mScaleFactor [protected] |
Scale factor to multiply the integrals
Definition at line 66 of file NaturalNeumannSurfaceTermAssembler.hpp.
Referenced by NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ComputeVectorSurfaceTerm(), and NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, 1 >::SetScaleFactor().
The documentation for this class was generated from the following file:
- pde/src/solver/NaturalNeumannSurfaceTermAssembler.hpp
 1.6.2
1.6.2