SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM > Class Template Reference

#include <SimpleNonlinearEllipticSolver.hpp>

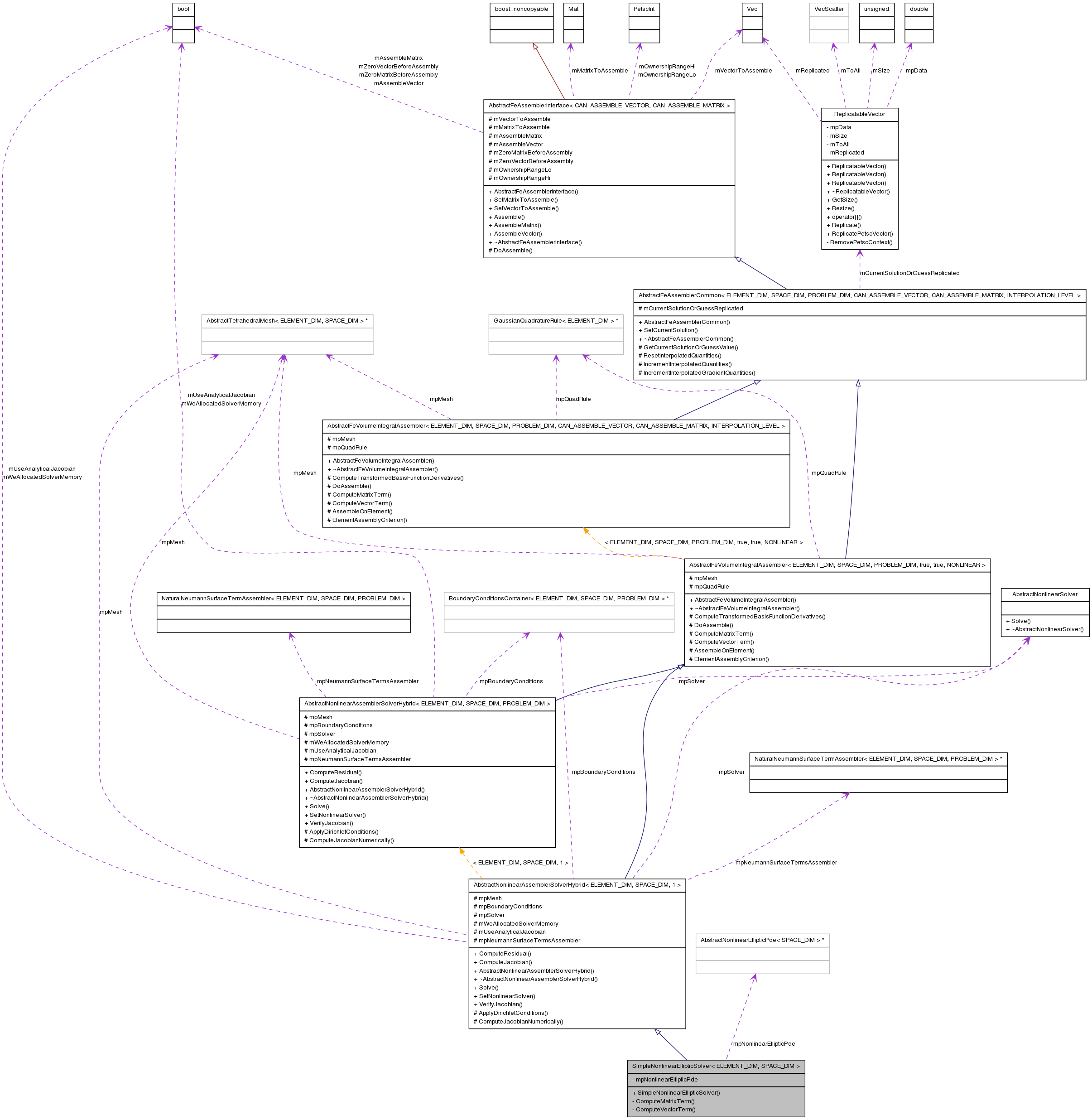
Inherits AbstractNonlinearAssemblerSolverHybrid< ELEMENT_DIM, SPACE_DIM, 1 >.

Collaboration diagram for SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >:

[legend]

List of all members.

Public Member Functions
	SimpleNonlinearEllipticSolver (AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *pMesh, AbstractNonlinearEllipticPde< SPACE_DIM > *pPde, BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 1 > *pBoundaryConditions)
Private Member Functions
virtual c_matrix< double, 1 *(ELEMENT_DIM+1), 1 *(ELEMENT_DIM+1)>	ComputeMatrixTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, 1 > &rU, c_matrix< double, 1, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement)
virtual c_vector< double, 1 *(ELEMENT_DIM+1)>	ComputeVectorTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, 1 > &rU, c_matrix< double, 1, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement)
Private Attributes
AbstractNonlinearEllipticPde < SPACE_DIM > *	mpNonlinearEllipticPde

---

Detailed Description

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
class SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >

Solver of nonlinear elliptic PDEs.

Definition at line 46 of file SimpleNonlinearEllipticSolver.hpp.

---

Constructor & Destructor Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>

SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::SimpleNonlinearEllipticSolver	(	AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *	pMesh,
		AbstractNonlinearEllipticPde< SPACE_DIM > *	pPde,
		BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 1 > *	pBoundaryConditions
	)			[inline]

Constructor.

Parameters:

	pMesh	pointer to the mesh
	pPde	pointer to the PDE
	pBoundaryConditions	pointer to the boundary conditions

Definition at line 102 of file SimpleNonlinearEllipticSolver.cpp.

---

Member Function Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>

c_matrix< double, 1 *(ELEMENT_DIM+1), 1 *(ELEMENT_DIM+1)> SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeMatrixTerm	(	c_vector< double, ELEMENT_DIM+1 > &	rPhi,
		c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &	rGradPhi,
		ChastePoint< SPACE_DIM > &	rX,
		c_vector< double, 1 > &	rU,
		c_matrix< double, 1, SPACE_DIM > &	rGradU,
		Element< ELEMENT_DIM, SPACE_DIM > *	pElement
	)			[inline, private, virtual]

Returns:

the matrix to be added to element stiffness matrix for a given Gauss point. The arguments are the bases, bases gradients, x and current solution computed at the Gauss point. The returned matrix will be multiplied by the Gauss weight and Jacobian determinant and added to the element stiffness matrix (see AssembleOnElement()).

Parameters:

	rPhi	The basis functions, rPhi(i) = phi_i, i=1..numBases
	rGradPhi	Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i)
	rX	The point in space
	rU	The unknown as a vector, u(i) = u_i
	rGradU	The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j)
	pElement	Pointer to the element

Definition at line 39 of file SimpleNonlinearEllipticSolver.cpp.

References SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde.

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>

c_vector< double, 1 *(ELEMENT_DIM+1)> SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeVectorTerm	(	c_vector< double, ELEMENT_DIM+1 > &	rPhi,
		c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &	rGradPhi,
		ChastePoint< SPACE_DIM > &	rX,
		c_vector< double, 1 > &	rU,
		c_matrix< double, 1, SPACE_DIM > &	rGradU,
		Element< ELEMENT_DIM, SPACE_DIM > *	pElement
	)			[inline, private, virtual]

Returns:

the vector to be added to element stiffness vector for a given Gauss point. The arguments are the bases, x and current solution computed at the Gauss point. The returned vector will be multiplied by the Gauss weight and Jacobian determinant and added to the element stiffness matrix (see AssembleOnElement()).

Parameters:

	rPhi	The basis functions, rPhi(i) = phi_i, i=1..numBases
	rGradPhi	Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i)
	rX	The point in space
	rU	The unknown as a vector, u(i) = u_i
	rGradU	The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j)
	pElement	Pointer to the element

Definition at line 72 of file SimpleNonlinearEllipticSolver.cpp.

References SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde.

---

Member Data Documentation

template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>

AbstractNonlinearEllipticPde<SPACE_DIM>* SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::mpNonlinearEllipticPde [private]

The PDE to be solved.

Definition at line 51 of file SimpleNonlinearEllipticSolver.hpp.

Referenced by SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeMatrixTerm(), and SimpleNonlinearEllipticSolver< ELEMENT_DIM, SPACE_DIM >::ComputeVectorTerm().

---

The documentation for this class was generated from the following files:

• pde/src/solver/SimpleNonlinearEllipticSolver.hpp
• pde/src/solver/SimpleNonlinearEllipticSolver.cpp