#include <StokesFlowAssembler.hpp>
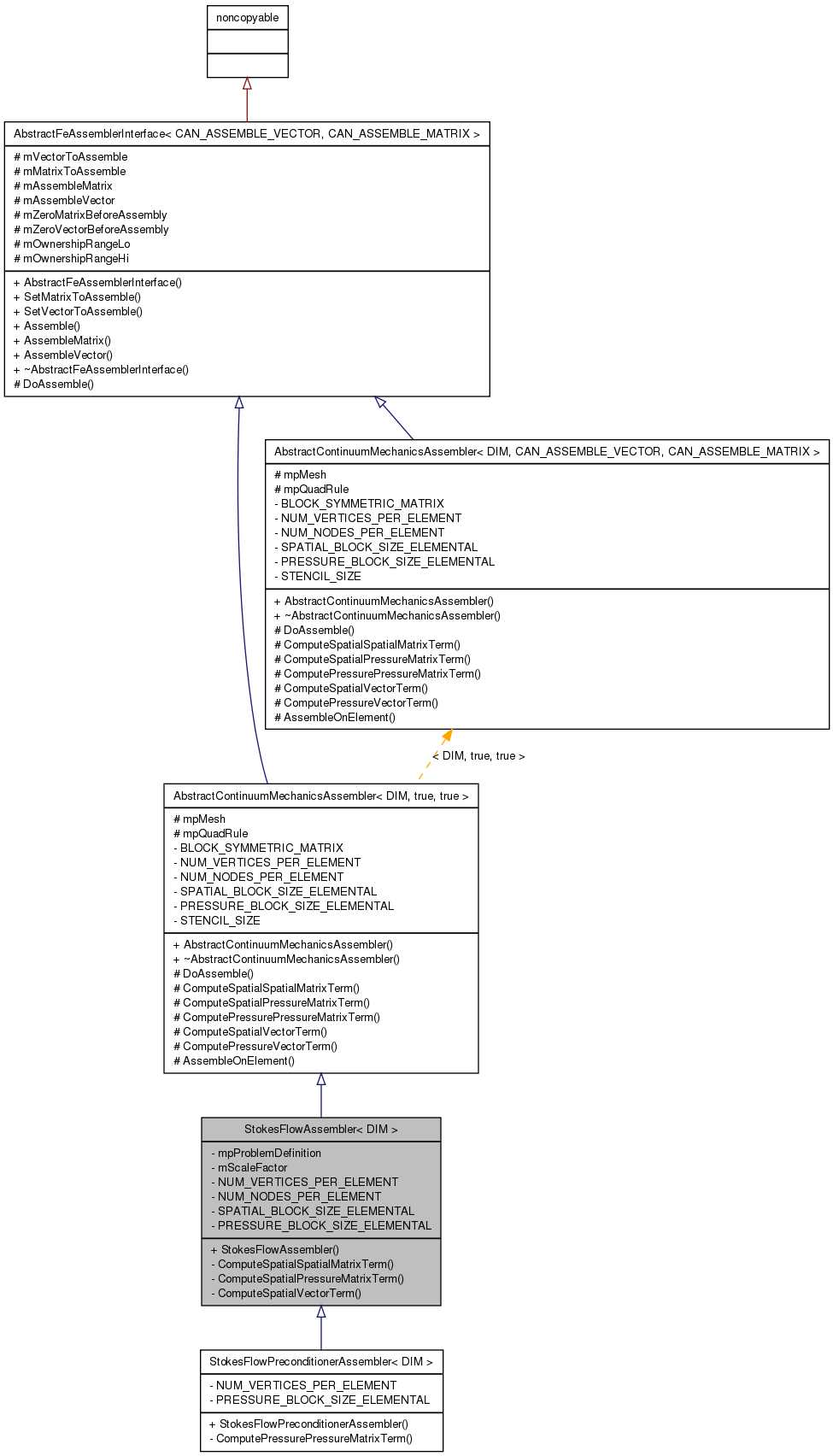
 Inheritance diagram for StokesFlowAssembler< DIM >:
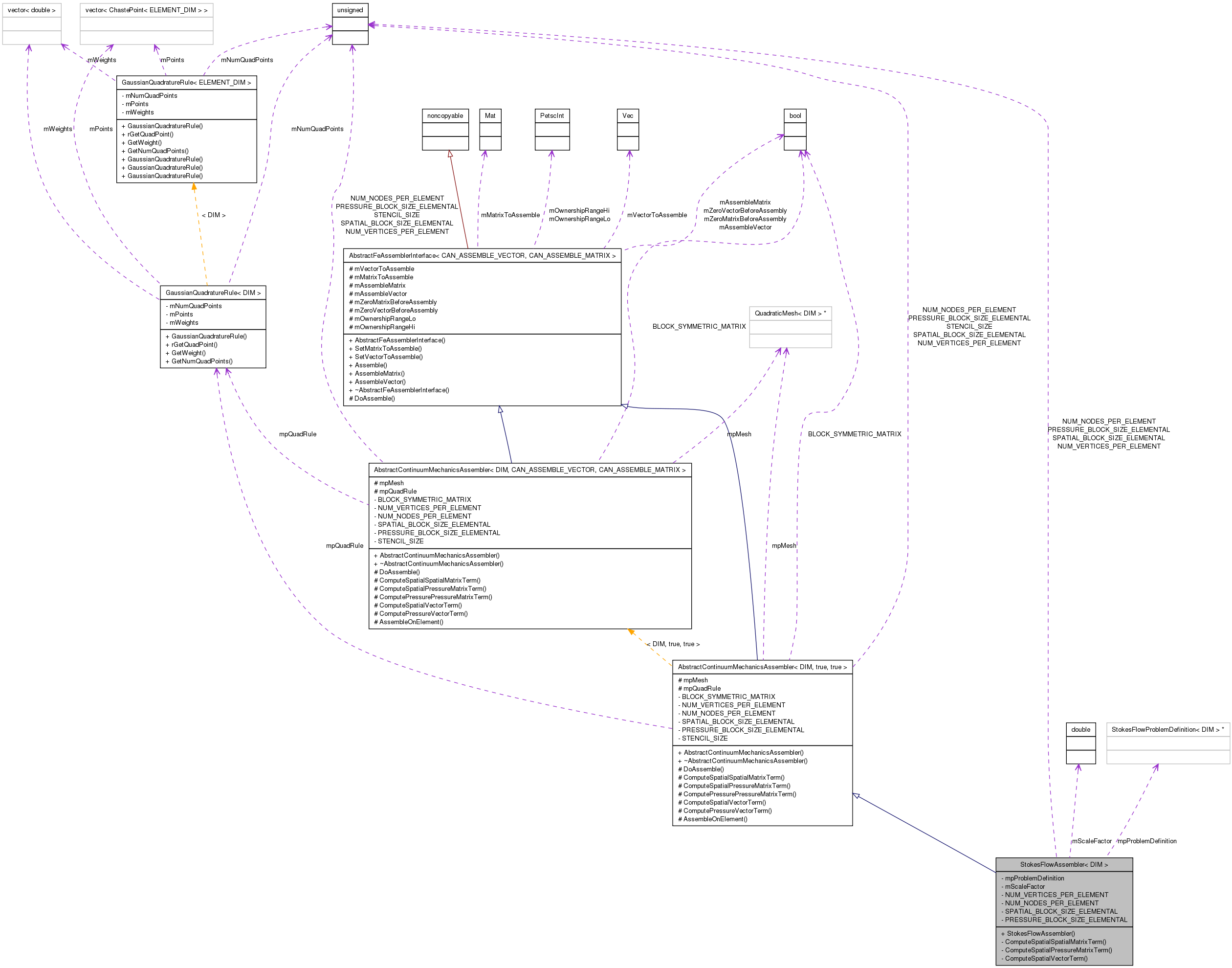
Inheritance diagram for StokesFlowAssembler< DIM >: Collaboration diagram for StokesFlowAssembler< DIM >:
Collaboration diagram for StokesFlowAssembler< DIM >:Detailed Description
template<unsigned DIM>
class StokesFlowAssembler< DIM >
Assembler for setting up (volume-integral parts of) the matrix and vector used in the FEM discretisation of Stokes' Flow.
The matrix has the block-form (except see comment below) [A B] [B^T 0] and the vector has the block form (except see comment below) [b] [0]
NOTE: The elemental matrix and vector is as above. The full matrix and vector uses a completely different ordering: for parallelisation reasons the pressure variables are interleaved with the spatial variables and dummy pressure variables are used for internal nodes. For example, in 2d, the ordering is [U1 V1 P1 , .. , Un Vn, Pn] where n is the total number of nodes.
Definition at line 62 of file StokesFlowAssembler.hpp.
Constructor & Destructor Documentation
| StokesFlowAssembler< DIM >::StokesFlowAssembler | ( | QuadraticMesh< DIM > * | pMesh, |
| StokesFlowProblemDefinition< DIM > * | pProblemDefinition | ||
| ) | [inline] |
Constructor
- Parameters:
-
pMesh pProblemDefinition
Definition at line 248 of file StokesFlowAssembler.hpp.
Member Function Documentation
| c_matrix<double,SPATIAL_BLOCK_SIZE_ELEMENTAL,PRESSURE_BLOCK_SIZE_ELEMENTAL> StokesFlowAssembler< DIM >::ComputeSpatialPressureMatrixTerm | ( | c_vector< double, NUM_NODES_PER_ELEMENT > & | rQuadPhi, |
| c_matrix< double, DIM, NUM_NODES_PER_ELEMENT > & | rGradQuadPhi, | ||
| c_vector< double, NUM_VERTICES_PER_ELEMENT > & | rLinearPhi, | ||
| c_matrix< double, DIM, NUM_VERTICES_PER_ELEMENT > & | rGradLinearPhi, | ||
| c_vector< double, DIM > & | rX, | ||
| Element< DIM, DIM > * | pElement | ||
| ) | [inline, private, virtual] |
The matrix has the form (except see comments about ordering above) [A B ] [B^T 0 ] The function is related to the spatial-pressure block, ie matrix B.
For the (volume-integral) contribution to B from a given element, this method returns the INTEGRAND in the definition of B.
- Parameters:
-
rQuadPhi All the quadratic basis functions on this element, evaluated at the current quad point rGradQuadPhi Gradients of all the quadratic basis functions on this element, evaluated at the current quad point rLinearPhi All the linear basis functions on this element, evaluated at the current quad point rGradLinearPhi Gradients of all the linear basis functions on this element, evaluated at the current quad point rX Current location (physical position corresponding to quad point) pElement Current element
Reimplemented from AbstractContinuumMechanicsAssembler< DIM, true, true >.
Definition at line 166 of file StokesFlowAssembler.hpp.
References StokesFlowAssembler< DIM >::NUM_NODES_PER_ELEMENT, StokesFlowAssembler< DIM >::NUM_VERTICES_PER_ELEMENT, StokesFlowAssembler< DIM >::PRESSURE_BLOCK_SIZE_ELEMENTAL, and StokesFlowAssembler< DIM >::SPATIAL_BLOCK_SIZE_ELEMENTAL.
| c_matrix<double,SPATIAL_BLOCK_SIZE_ELEMENTAL,SPATIAL_BLOCK_SIZE_ELEMENTAL> StokesFlowAssembler< DIM >::ComputeSpatialSpatialMatrixTerm | ( | c_vector< double, NUM_NODES_PER_ELEMENT > & | rQuadPhi, |
| c_matrix< double, DIM, NUM_NODES_PER_ELEMENT > & | rGradQuadPhi, | ||
| c_vector< double, DIM > & | rX, | ||
| Element< DIM, DIM > * | pElement | ||
| ) | [inline, private, virtual] |
The matrix has the form (except see comments about ordering above) [A B ] [B^T 0 ] The function is related to the spatial-spatial block, ie matrix A.
For the (volume-integral) contribution to A from a given element, this method returns the INTEGRAND in the definition of A.
- Parameters:
-
rQuadPhi All the quadratic basis functions on this element, evaluated at the current quad point rGradQuadPhi Gradients of all the quadratic basis functions on this element, evaluated at the current quad point rX Current location (physical position corresponding to quad point) pElement Current element
Reimplemented from AbstractContinuumMechanicsAssembler< DIM, true, true >.
Definition at line 112 of file StokesFlowAssembler.hpp.
References StokesFlowAssembler< DIM >::mpProblemDefinition, StokesFlowAssembler< DIM >::mScaleFactor, StokesFlowAssembler< DIM >::NUM_NODES_PER_ELEMENT, and StokesFlowAssembler< DIM >::SPATIAL_BLOCK_SIZE_ELEMENTAL.
| c_vector<double,SPATIAL_BLOCK_SIZE_ELEMENTAL> StokesFlowAssembler< DIM >::ComputeSpatialVectorTerm | ( | c_vector< double, NUM_NODES_PER_ELEMENT > & | rQuadPhi, |
| c_matrix< double, DIM, NUM_NODES_PER_ELEMENT > & | rGradQuadPhi, | ||
| c_vector< double, DIM > & | rX, | ||
| Element< DIM, DIM > * | pElement | ||
| ) | [inline, private, virtual] |
The matrix has the form (except see comments about ordering above) [A B ] [B^T 0 ] and the vector has the form [b1] [b2] The function is related to the spatial-block in the vector, ie b1.
For the contribution to b1 from a given element, this method should return the INTEGRAND in the definition of b1.
- Parameters:
-
rQuadPhi All the quadratic basis functions on this element, evaluated at the current quad point rGradQuadPhi Gradients of all the quadratic basis functions on this element, evaluated at the current quad point rX Current location (physical position) pElement Current element
Reimplemented from AbstractContinuumMechanicsAssembler< DIM, true, true >.
Definition at line 214 of file StokesFlowAssembler.hpp.
References StokesFlowAssembler< DIM >::mpProblemDefinition, StokesFlowAssembler< DIM >::NUM_NODES_PER_ELEMENT, and StokesFlowAssembler< DIM >::SPATIAL_BLOCK_SIZE_ELEMENTAL.
Member Data Documentation
StokesFlowProblemDefinition<DIM>* StokesFlowAssembler< DIM >::mpProblemDefinition [private] |
Stokes' flow problem definition
Definition at line 86 of file StokesFlowAssembler.hpp.
Referenced by StokesFlowAssembler< DIM >::ComputeSpatialSpatialMatrixTerm(), and StokesFlowAssembler< DIM >::ComputeSpatialVectorTerm().
double StokesFlowAssembler< DIM >::mScaleFactor [private] |
This variable is initialised to 1.0 and almost never changed, and is used in the spatial-spatial matrix term. One test (see TestStokesFlowAssembler) sets it to 0.0 before assembling the matrix. Basically, a different weak form USED to be implemented here (corresponding to one kind of Neumann boundary condition), and the matrix for that weak form was compared against exact solutions in this test. mScaleFactor = 0.0 corresponds to old weak form, mScaleFactor = 1 corresponds to new weak form as documented in fem implementations pdf.
Definition at line 95 of file StokesFlowAssembler.hpp.
Referenced by StokesFlowAssembler< DIM >::ComputeSpatialSpatialMatrixTerm().
const unsigned StokesFlowAssembler< DIM >::NUM_NODES_PER_ELEMENT = (DIM+1)*(DIM+2)/2 [static, private] |
Number of nodes per element.
Reimplemented from AbstractContinuumMechanicsAssembler< DIM, true, true >.
Definition at line 71 of file StokesFlowAssembler.hpp.
Referenced by StokesFlowAssembler< DIM >::ComputeSpatialPressureMatrixTerm(), StokesFlowAssembler< DIM >::ComputeSpatialSpatialMatrixTerm(), and StokesFlowAssembler< DIM >::ComputeSpatialVectorTerm().
const unsigned StokesFlowAssembler< DIM >::NUM_VERTICES_PER_ELEMENT = DIM+1 [static, private] |
Number of vertices per element
Reimplemented from AbstractContinuumMechanicsAssembler< DIM, true, true >.
Reimplemented in StokesFlowPreconditionerAssembler< DIM >.
Definition at line 68 of file StokesFlowAssembler.hpp.
Referenced by StokesFlowAssembler< DIM >::ComputeSpatialPressureMatrixTerm().
const unsigned StokesFlowAssembler< DIM >::PRESSURE_BLOCK_SIZE_ELEMENTAL = NUM_VERTICES_PER_ELEMENT [static, private] |
Size of the pressure block, per element, equal num_vertices times 1 (as p solved for at each vertex.
Reimplemented from AbstractContinuumMechanicsAssembler< DIM, true, true >.
Reimplemented in StokesFlowPreconditionerAssembler< DIM >.
Definition at line 83 of file StokesFlowAssembler.hpp.
Referenced by StokesFlowAssembler< DIM >::ComputeSpatialPressureMatrixTerm().
const unsigned StokesFlowAssembler< DIM >::SPATIAL_BLOCK_SIZE_ELEMENTAL = DIM*NUM_NODES_PER_ELEMENT [static, private] |
Size of the spatial block, per element, equal num_nodes times DIM (as say in 2d (u,v) solved for at each node
Reimplemented from AbstractContinuumMechanicsAssembler< DIM, true, true >.
Definition at line 77 of file StokesFlowAssembler.hpp.
Referenced by StokesFlowAssembler< DIM >::ComputeSpatialPressureMatrixTerm(), StokesFlowAssembler< DIM >::ComputeSpatialSpatialMatrixTerm(), and StokesFlowAssembler< DIM >::ComputeSpatialVectorTerm().
The documentation for this class was generated from the following file:
- continuum_mechanics/src/solver/StokesFlowAssembler.hpp