BidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM > Class Template Reference
#include <BidomainNeumannSurfaceTermAssembler.hpp>
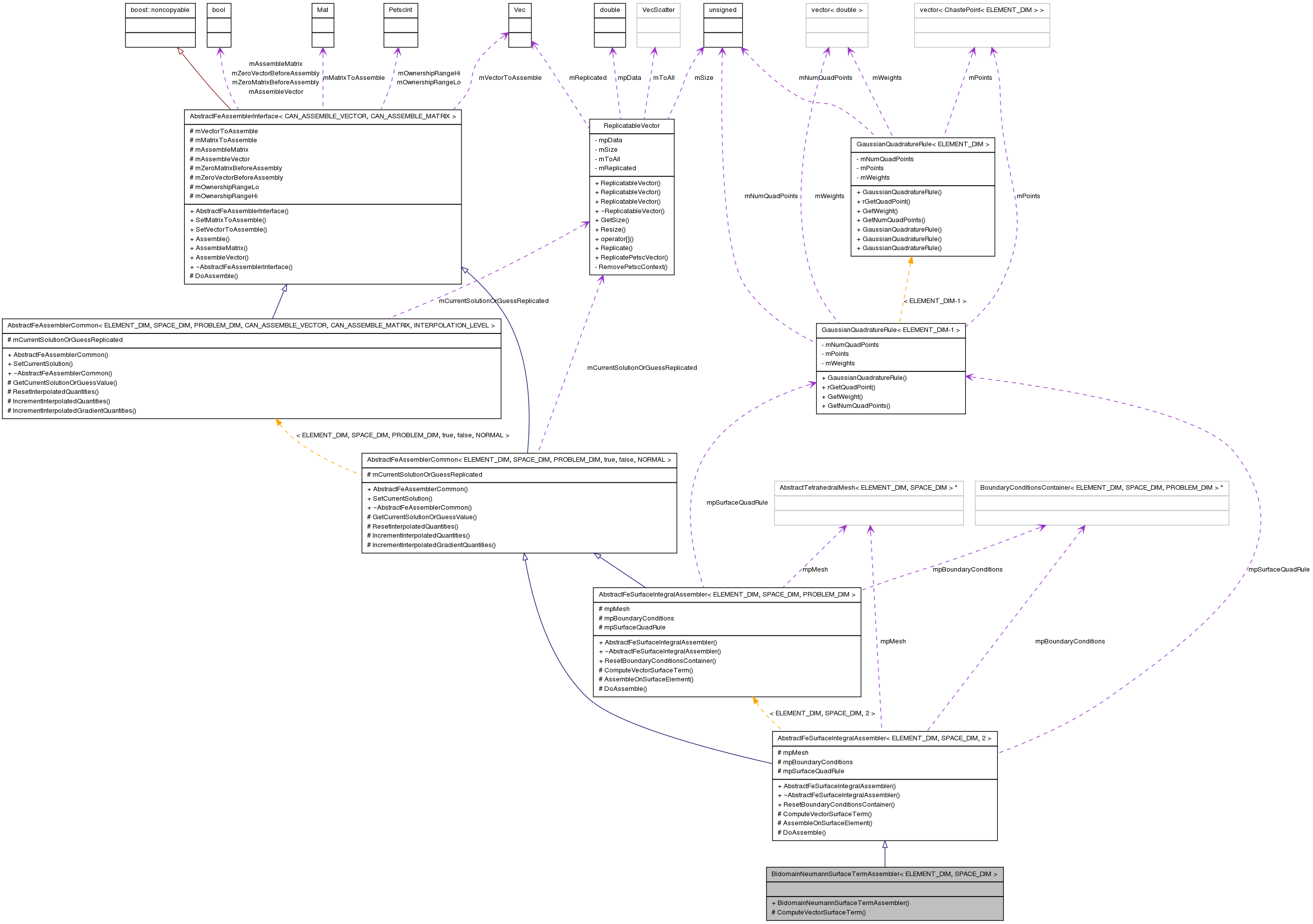
Inherits AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, 2 >.
Public Member Functions | |
| BidomainNeumannSurfaceTermAssembler (AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *pMesh, BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 2 > *pBoundaryConditions) | |
Protected Member Functions | |
| virtual c_vector< double, 2 *ELEMENT_DIM > | ComputeVectorSurfaceTerm (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, ELEMENT_DIM > &rPhi, ChastePoint< SPACE_DIM > &rX) |
Detailed Description
template<unsigned ELEMENT_DIM, unsigned SPACE_DIM>
class BidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM >
Assembler which sets up the surface integral integrals for the bidomain equations, assuming that the boundary conditions are written: div(sigma_i grad phi_i) . n = g1 and div(sigma_e grad phi_e) dot n = g2.
These are not 'natural' boundary conditions for the para-elliptic bidomain equations (natural BCs for the second
Hence we don't use the NaturalNeumannSurfaceTermAssembler and have a special class here. It means that any BCs specified for bidomain and put in a BoundaryConditionsContainer should be for div(sigma_i grad phi_i) . n and div(sigma_e grad phi_e) . n.
Definition at line 56 of file BidomainNeumannSurfaceTermAssembler.hpp.
Constructor & Destructor Documentation
| BidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM >::BidomainNeumannSurfaceTermAssembler | ( | AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > * | pMesh, | |
| BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, 2 > * | pBoundaryConditions | |||
| ) | [inline] |
Constructor
- Parameters:
-
pMesh The mesh pBoundaryConditions The boundary conditions container
Definition at line 83 of file BidomainNeumannSurfaceTermAssembler.hpp.
Member Function Documentation
| c_vector< double, 2 *ELEMENT_DIM > BidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM >::ComputeVectorSurfaceTerm | ( | const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > & | rSurfaceElement, | |
| c_vector< double, ELEMENT_DIM > & | rPhi, | |||
| ChastePoint< SPACE_DIM > & | rX | |||
| ) | [inline, protected, virtual] |
This method returns the vector to be added to full vector for a given Gauss point in BoundaryElement, ie, essentially the INTEGRAND in the boundary integral part of the definition of the vector. The arguments are the bases, x and current solution computed at the Gauss point.
- Parameters:
-
rSurfaceElement the element which is being considered. rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases rX The point in space
- Returns:
- stencil vector
Reimplemented from AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, 2 >.
Definition at line 93 of file BidomainNeumannSurfaceTermAssembler.hpp.
References AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, 2 >::mpBoundaryConditions.
The documentation for this class was generated from the following file:
- heart/src/solver/electrics/bidomain/BidomainNeumannSurfaceTermAssembler.hpp
 1.6.2
1.6.2