GaussianQuadratureRule< ELEMENT_DIM > Class Template Reference
#include <GaussianQuadratureRule.hpp>
Public Member Functions | |
| GaussianQuadratureRule (unsigned quadratureOrder) | |
| const ChastePoint< ELEMENT_DIM > & | rGetQuadPoint (unsigned index) const |
| double | GetWeight (unsigned index) const |
| unsigned | GetNumQuadPoints () const |
| template<> | |
| GaussianQuadratureRule (unsigned quadratureOrder) | |
| template<> | |
| GaussianQuadratureRule (unsigned quadratureOrder) | |
| template<> | |
| GaussianQuadratureRule (unsigned quadratureOrder) | |
Private Attributes | |
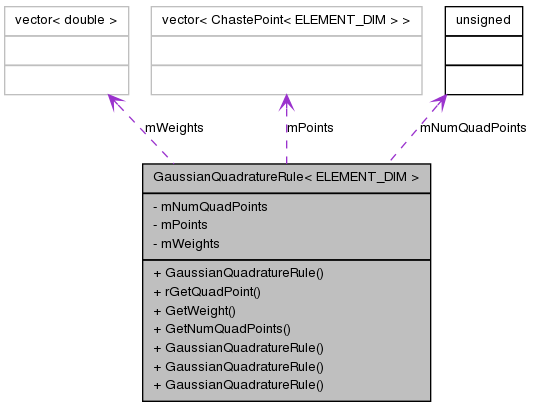
| unsigned | mNumQuadPoints |
| std::vector< ChastePoint < ELEMENT_DIM > > | mPoints |
| std::vector< double > | mWeights |
Detailed Description
template<unsigned ELEMENT_DIM>
class GaussianQuadratureRule< ELEMENT_DIM >
This class encapsulates tables of Gaussian quadrature points and the associated weights.
Data is available for 1d, 2d and 3d quadrature over (canonical) triangles, with appropriate numbers of Gauss points. Weights sum to 1 and are non-negative. The values are computed when an object is instantiated.
Definition at line 50 of file GaussianQuadratureRule.hpp.
Constructor & Destructor Documentation
| GaussianQuadratureRule< ELEMENT_DIM >::GaussianQuadratureRule | ( | unsigned | quadratureOrder | ) | [inline] |
The constructor builds the appropriate table for the dimension (given by the template argument) and number of points in each dimension (given as a constructor argument).
An exception is thrown if data is not available for the requested parameters.
- Parameters:
-
quadratureOrder The minimum polynomial order that the rule can integrate exactly
Definition at line 282 of file GaussianQuadratureRule.cpp.
References EXCEPTION.
| GaussianQuadratureRule< 0 >::GaussianQuadratureRule | ( | unsigned | quadratureOrder | ) | [inline] |
Constructor specialization for 0d.
- Parameters:
-
quadratureOrder The minimum polynomial order that the rule can integrate exactly (ignored in 0-d case)
Definition at line 68 of file GaussianQuadratureRule.cpp.
References GaussianQuadratureRule< ELEMENT_DIM >::mNumQuadPoints, GaussianQuadratureRule< ELEMENT_DIM >::mPoints, and GaussianQuadratureRule< ELEMENT_DIM >::mWeights.
| GaussianQuadratureRule< 2 >::GaussianQuadratureRule | ( | unsigned | quadratureOrder | ) | [inline] |
Constructor specialization for 2d.
- Parameters:
-
quadratureOrder The minimum polynomial order that the rule can integrate exactly
Definition at line 130 of file GaussianQuadratureRule.cpp.
References EXCEPTION, GaussianQuadratureRule< ELEMENT_DIM >::mNumQuadPoints, GaussianQuadratureRule< ELEMENT_DIM >::mPoints, and GaussianQuadratureRule< ELEMENT_DIM >::mWeights.
| GaussianQuadratureRule< 3 >::GaussianQuadratureRule | ( | unsigned | quadratureOrder | ) | [inline] |
Constructor specialization for 3d.
- Parameters:
-
quadratureOrder The minimum polynomial order that the rule can integrate exactly
Definition at line 198 of file GaussianQuadratureRule.cpp.
References EXCEPTION, GaussianQuadratureRule< ELEMENT_DIM >::mNumQuadPoints, GaussianQuadratureRule< ELEMENT_DIM >::mPoints, and GaussianQuadratureRule< ELEMENT_DIM >::mWeights.
Member Function Documentation
| unsigned GaussianQuadratureRule< ELEMENT_DIM >::GetNumQuadPoints | ( | ) | const [inline] |
- Returns:
- the number of quadrature points. This is the number of points in each dimension, raised to the power of the number of dimensions.
Definition at line 57 of file GaussianQuadratureRule.cpp.
References GaussianQuadratureRule< ELEMENT_DIM >::mNumQuadPoints.
Referenced by ContinuumMechanicsNeumannBcsAssembler< DIM >::AssembleOnBoundaryElement(), AbstractNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), AbstractNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElementForPressureOnDeformedBc(), AbstractFeCableIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::AssembleOnCableElement(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), AbstractContinuumMechanicsAssembler< DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX >::AssembleOnElement(), AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AssembleOnSurfaceElement(), AbstractFunctionalCalculator< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::CalculateOnElement(), ElectrodesStimulusFactory< DIM >::ComputeElectrodeTotalFlux(), and QuadraturePointsGroup< DIM >::QuadraturePointsGroup().
| double GaussianQuadratureRule< ELEMENT_DIM >::GetWeight | ( | unsigned | index | ) | const [inline] |
- Returns:
- the weight associated with a quadrature point.
- Parameters:
-
index The index of the point to return.
Definition at line 50 of file GaussianQuadratureRule.cpp.
References GaussianQuadratureRule< ELEMENT_DIM >::mNumQuadPoints, and GaussianQuadratureRule< ELEMENT_DIM >::mWeights.
Referenced by ContinuumMechanicsNeumannBcsAssembler< DIM >::AssembleOnBoundaryElement(), AbstractNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), AbstractNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElementForPressureOnDeformedBc(), AbstractFeCableIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::AssembleOnCableElement(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), AbstractContinuumMechanicsAssembler< DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX >::AssembleOnElement(), AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AssembleOnSurfaceElement(), AbstractFunctionalCalculator< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::CalculateOnElement(), and ElectrodesStimulusFactory< DIM >::ComputeElectrodeTotalFlux().
| const ChastePoint< ELEMENT_DIM > & GaussianQuadratureRule< ELEMENT_DIM >::rGetQuadPoint | ( | unsigned | index | ) | const [inline] |
Get a quadrature point.
- Parameters:
-
index The index of the point to return.
- Returns:
- A gaussian quadrature point.
Definition at line 43 of file GaussianQuadratureRule.cpp.
References GaussianQuadratureRule< ELEMENT_DIM >::mNumQuadPoints, and GaussianQuadratureRule< ELEMENT_DIM >::mPoints.
Referenced by ContinuumMechanicsNeumannBcsAssembler< DIM >::AssembleOnBoundaryElement(), AbstractNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElement(), AbstractNonlinearElasticitySolver< DIM >::AssembleOnBoundaryElementForPressureOnDeformedBc(), AbstractFeCableIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::AssembleOnCableElement(), IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), AbstractContinuumMechanicsAssembler< DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX >::AssembleOnElement(), AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AssembleOnSurfaceElement(), AbstractFunctionalCalculator< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::CalculateOnElement(), ElectrodesStimulusFactory< DIM >::ComputeElectrodeTotalFlux(), and QuadraturePointsGroup< DIM >::QuadraturePointsGroup().
Member Data Documentation
unsigned GaussianQuadratureRule< ELEMENT_DIM >::mNumQuadPoints [private] |
The total number of Gauss points.
Definition at line 53 of file GaussianQuadratureRule.hpp.
Referenced by GaussianQuadratureRule< 1 >::GaussianQuadratureRule(), GaussianQuadratureRule< ELEMENT_DIM >::GaussianQuadratureRule(), GaussianQuadratureRule< ELEMENT_DIM >::GetNumQuadPoints(), GaussianQuadratureRule< ELEMENT_DIM >::GetWeight(), and GaussianQuadratureRule< ELEMENT_DIM >::rGetQuadPoint().
std::vector<ChastePoint<ELEMENT_DIM> > GaussianQuadratureRule< ELEMENT_DIM >::mPoints [private] |
The gaussian quadrature points.
Definition at line 56 of file GaussianQuadratureRule.hpp.
Referenced by GaussianQuadratureRule< 1 >::GaussianQuadratureRule(), GaussianQuadratureRule< ELEMENT_DIM >::GaussianQuadratureRule(), and GaussianQuadratureRule< ELEMENT_DIM >::rGetQuadPoint().
std::vector<double> GaussianQuadratureRule< ELEMENT_DIM >::mWeights [private] |
The associated weights.
Definition at line 59 of file GaussianQuadratureRule.hpp.
Referenced by GaussianQuadratureRule< 1 >::GaussianQuadratureRule(), GaussianQuadratureRule< ELEMENT_DIM >::GaussianQuadratureRule(), and GaussianQuadratureRule< ELEMENT_DIM >::GetWeight().
The documentation for this class was generated from the following files:
- pde/src/solver/GaussianQuadratureRule.hpp
- pde/src/solver/GaussianQuadratureRule.cpp
 1.6.2
1.6.2