#include <AbstractFeVolumeIntegralAssembler.hpp>
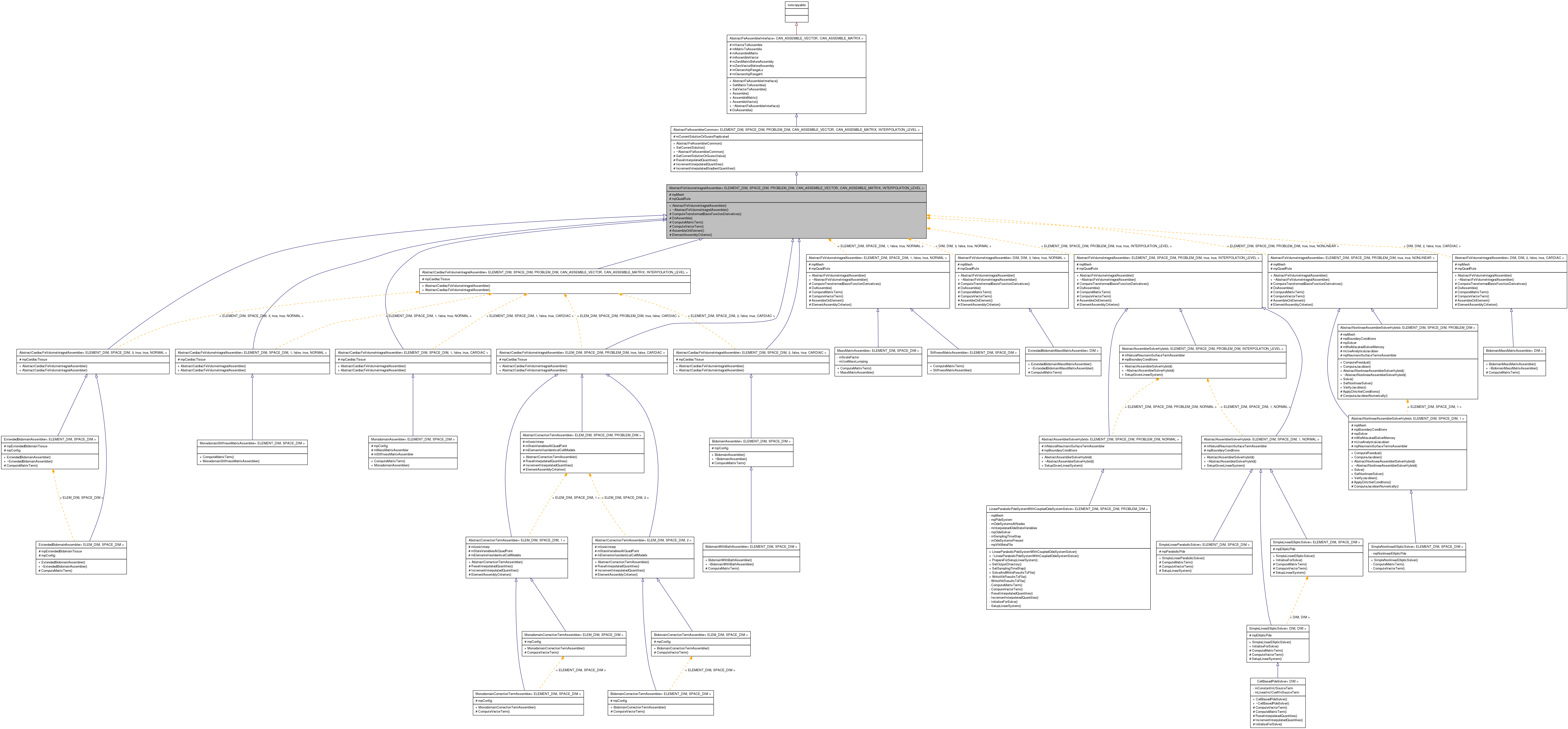
 Inheritance diagram for AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >:
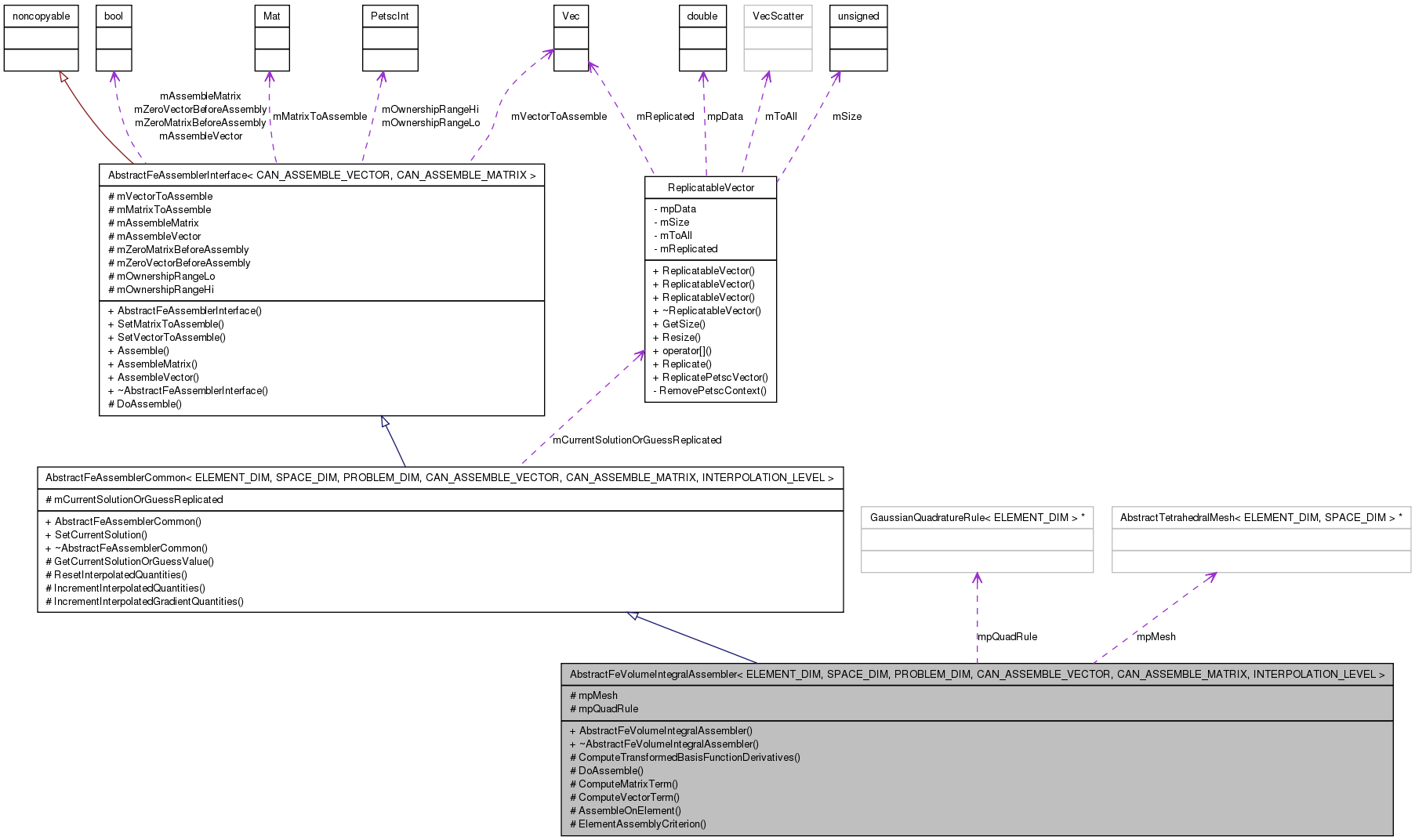
Inheritance diagram for AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >: Collaboration diagram for AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >:
Collaboration diagram for AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >:Public Member Functions | |
| AbstractFeVolumeIntegralAssembler (AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *pMesh, unsigned numQuadPoints=2) | |
| virtual | ~AbstractFeVolumeIntegralAssembler () |
Protected Types | |
| typedef LinearBasisFunction < ELEMENT_DIM > | BasisFunction |
Protected Member Functions | |
| void | ComputeTransformedBasisFunctionDerivatives (const ChastePoint< ELEMENT_DIM > &rPoint, const c_matrix< double, ELEMENT_DIM, SPACE_DIM > &rInverseJacobian, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rReturnValue) |
| void | DoAssemble () |
| virtual c_matrix< double, PROBLEM_DIM *(ELEMENT_DIM+1), PROBLEM_DIM *(ELEMENT_DIM+1)> | ComputeMatrixTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, PROBLEM_DIM > &rU, c_matrix< double, PROBLEM_DIM, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement) |
| virtual c_vector< double, PROBLEM_DIM *(ELEMENT_DIM+1)> | ComputeVectorTerm (c_vector< double, ELEMENT_DIM+1 > &rPhi, c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > &rGradPhi, ChastePoint< SPACE_DIM > &rX, c_vector< double, PROBLEM_DIM > &rU, c_matrix< double, PROBLEM_DIM, SPACE_DIM > &rGradU, Element< ELEMENT_DIM, SPACE_DIM > *pElement) |
| virtual void | AssembleOnElement (Element< ELEMENT_DIM, SPACE_DIM > &rElement, c_matrix< double, PROBLEM_DIM *(ELEMENT_DIM+1), PROBLEM_DIM *(ELEMENT_DIM+1) > &rAElem, c_vector< double, PROBLEM_DIM *(ELEMENT_DIM+1)> &rBElem) |
| virtual bool | ElementAssemblyCriterion (Element< ELEMENT_DIM, SPACE_DIM > &rElement) |
Protected Attributes | |
| AbstractTetrahedralMesh < ELEMENT_DIM, SPACE_DIM > * | mpMesh |
| GaussianQuadratureRule < ELEMENT_DIM > * | mpQuadRule |
Detailed Description
template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM, bool CAN_ASSEMBLE_VECTOR, bool CAN_ASSEMBLE_MATRIX, InterpolationLevel INTERPOLATION_LEVEL>
class AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >
An abstract class for creating finite element vectors or matrices that are defined by integrals over the computational domain of functions of basis functions (for example, stiffness or mass matrices), that require assembly by looping over each element in the mesh and computing the element-wise integrals and adding it to the full matrix or vector.
This class is used for VOLUME integrals. For surface integrals there is a similar class, AbstractFeSurfaceIntegralAssembler.
This class can be used to assemble a matrix OR a vector OR one of each. The template booleans CAN_ASSEMBLE_VECTOR and CAN_ASSEMBLE_MATRIX should be chosen accordingly.
The class provides the functionality to loop over elements, perform element-wise integration (using Gaussian quadrature and linear basis functions), and add the results to the final matrix or vector. The concrete class which inherits from this must implement either COMPUTE_MATRIX_TERM or COMPUTE_VECTOR_TERM or both, which should return the INTEGRAND, as a function of the basis functions.
The final template parameter defines how much interpolation (onto quadrature points) is required by the concrete class.
CARDIAC: only interpolates the first component of the unknown (ie the voltage) NORMAL: interpolates the position X and all components of the unknown u NONLINEAR: interpolates X, u and grad(u). Also computes the gradient of the basis functions when assembling vectors.
This class inherits from AbstractFeAssemblerCommon which is where some member variables (the matrix/vector to be created, for example) are defined.
Definition at line 78 of file AbstractFeVolumeIntegralAssembler.hpp.
Member Typedef Documentation
typedef LinearBasisFunction<ELEMENT_DIM> AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::BasisFunction [protected] |
Basis function for use with normal elements.
Definition at line 89 of file AbstractFeVolumeIntegralAssembler.hpp.
Constructor & Destructor Documentation
| AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::AbstractFeVolumeIntegralAssembler | ( | AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > * | pMesh, |
| unsigned | numQuadPoints = 2 |
||
| ) |
Constructor.
- Parameters:
-
pMesh The mesh numQuadPoints The number of quadratures points (in each dimension) to use per element. Defaults to 2.
Definition at line 242 of file AbstractFeVolumeIntegralAssembler.hpp.
| virtual AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::~AbstractFeVolumeIntegralAssembler | ( | ) | [inline, virtual] |
Destructor.
Definition at line 235 of file AbstractFeVolumeIntegralAssembler.hpp.
Member Function Documentation
| void AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::AssembleOnElement | ( | Element< ELEMENT_DIM, SPACE_DIM > & | rElement, |
| c_matrix< double, PROBLEM_DIM *(ELEMENT_DIM+1), PROBLEM_DIM *(ELEMENT_DIM+1) > & | rAElem, | ||
| c_vector< double, PROBLEM_DIM *(ELEMENT_DIM+1)> & | rBElem | ||
| ) | [protected, virtual] |
Calculate the contribution of a single element to the linear system.
- Parameters:
-
rElement The element to assemble on. rAElem The element's contribution to the LHS matrix is returned in this n by n matrix, where n is the no. of nodes in this element. There is no need to zero this matrix before calling. rBElem The element's contribution to the RHS vector is returned in this vector of length n, the no. of nodes in this element. There is no need to zero this vector before calling.
Called by AssembleSystem(). Calls ComputeMatrixTerm() etc.
- Todo:
- #1320 This assumes that the Jacobian is constant on an element. This is true for linear basis functions, but not for any other type of basis function.
Definition at line 344 of file AbstractFeVolumeIntegralAssembler.hpp.
References AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetIndex(), AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetNode(), AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetNodeGlobalIndex(), AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetNumNodes(), ChastePoint< DIM >::rGetLocation(), and Node< SPACE_DIM >::rGetLocation().
| virtual c_matrix<double,PROBLEM_DIM*(ELEMENT_DIM+1),PROBLEM_DIM*(ELEMENT_DIM+1)> AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::ComputeMatrixTerm | ( | c_vector< double, ELEMENT_DIM+1 > & | rPhi, |
| c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > & | rGradPhi, | ||
| ChastePoint< SPACE_DIM > & | rX, | ||
| c_vector< double, PROBLEM_DIM > & | rU, | ||
| c_matrix< double, PROBLEM_DIM, SPACE_DIM > & | rGradU, | ||
| Element< ELEMENT_DIM, SPACE_DIM > * | pElement | ||
| ) | [inline, protected, virtual] |
This method returns the matrix to be added to element stiffness matrix for a given Gauss point, ie, essentially the INTEGRAND in the integral definition of the matrix. The arguments are the bases, bases gradients, x and current solution computed at the Gauss point. The returned matrix will be multiplied by the Gauss weight and Jacobian determinant and added to the element stiffness matrix (see AssembleOnElement()).
** This method has to be implemented in the concrete class if CAN_ASSEMBLE_MATRIX is true. **
NOTE: When INTERPOLATION_LEVEL==NORMAL, rGradU does not get set up and should not be used.
- Parameters:
-
rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases. rGradPhi Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i). rX The point in space. rU The unknown as a vector, u(i) = u_i. rGradU The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j). pElement Pointer to the element.
Reimplemented in LinearParabolicPdeSystemWithCoupledOdeSystemSolver< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >.
Definition at line 142 of file AbstractFeVolumeIntegralAssembler.hpp.
| void AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::ComputeTransformedBasisFunctionDerivatives | ( | const ChastePoint< ELEMENT_DIM > & | rPoint, |
| const c_matrix< double, ELEMENT_DIM, SPACE_DIM > & | rInverseJacobian, | ||
| c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > & | rReturnValue | ||
| ) | [protected] |
Compute the derivatives of all basis functions at a point within an element. This method will transform the results, for use within Gaussian quadrature for example.
This is almost identical to LinearBasisFunction::ComputeTransformedBasisFunctionDerivatives, except that it is also templated over SPACE_DIM and can handle cases such as 1d in 3d space.
- Todo:
- #1319 Template LinearBasisFunction over SPACE_DIM and remove this method?
- Parameters:
-
rPoint The point at which to compute the basis functions. The results are undefined if this is not within the canonical element. rInverseJacobian The inverse of the Jacobian matrix mapping the real element into the canonical element. rReturnValue A reference to a vector, to be filled in
- Returns:
- The derivatives of the basis functions, in local index order. Each entry is a vector (c_vector<double, SPACE_DIM> instance) giving the derivative along each axis.
Definition at line 331 of file AbstractFeVolumeIntegralAssembler.hpp.
References LinearBasisFunction< ELEMENT_DIM >::ComputeBasisFunctionDerivatives().
| virtual c_vector<double,PROBLEM_DIM*(ELEMENT_DIM+1)> AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::ComputeVectorTerm | ( | c_vector< double, ELEMENT_DIM+1 > & | rPhi, |
| c_matrix< double, SPACE_DIM, ELEMENT_DIM+1 > & | rGradPhi, | ||
| ChastePoint< SPACE_DIM > & | rX, | ||
| c_vector< double, PROBLEM_DIM > & | rU, | ||
| c_matrix< double, PROBLEM_DIM, SPACE_DIM > & | rGradU, | ||
| Element< ELEMENT_DIM, SPACE_DIM > * | pElement | ||
| ) | [inline, protected, virtual] |
This method returns the vector to be added to element stiffness vector for a given Gauss point, ie, essentially the INTEGRAND in the integral definition of the vector. The arguments are the bases, x and current solution computed at the Gauss point. The returned vector will be multiplied by the Gauss weight and Jacobian determinant and added to the element stiffness matrix (see AssembleOnElement()).
** This method has to be implemented in the concrete class if CAN_ASSEMBLE_VECTOR is true. **
NOTE: When INTERPOLATION_LEVEL==NORMAL, rGradPhi and rGradU do not get set up and should not be used.
- Parameters:
-
rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases rGradPhi Basis gradients, rGradPhi(i,j) = d(phi_j)/d(X_i) rX The point in space rU The unknown as a vector, u(i) = u_i rGradU The gradient of the unknown as a matrix, rGradU(i,j) = d(u_i)/d(X_j) pElement Pointer to the element
Reimplemented in LinearParabolicPdeSystemWithCoupledOdeSystemSolver< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >.
Definition at line 175 of file AbstractFeVolumeIntegralAssembler.hpp.
| void AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::DoAssemble | ( | ) | [protected, virtual] |
The main assembly method. Should only be called through Assemble(), AssembleMatrix() or AssembleVector() which set mAssembleMatrix, mAssembleVector accordingly.
Implements AbstractFeAssemblerInterface< CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX >.
Definition at line 256 of file AbstractFeVolumeIntegralAssembler.hpp.
References GenericEventHandler< 16, HeartEventHandler >::BeginEvent(), GenericEventHandler< 16, HeartEventHandler >::EndEvent(), EXCEPTION, AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetOwnership(), AbstractTetrahedralElement< ELEMENT_DIM, SPACE_DIM >::GetStiffnessMatrixGlobalIndices(), PetscMatTools::Zero(), and PetscVecTools::Zero().
| virtual bool AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::ElementAssemblyCriterion | ( | Element< ELEMENT_DIM, SPACE_DIM > & | rElement | ) | [inline, protected, virtual] |
Whether to include this (volume) element when assembling. Returns true here but can be overridden by the concrete assembler if not all elements should be included.
- Parameters:
-
rElement the element
Reimplemented in AbstractCorrectionTermAssembler< ELEM_DIM, SPACE_DIM, PROBLEM_DIM >.
Definition at line 215 of file AbstractFeVolumeIntegralAssembler.hpp.
Member Data Documentation
AbstractTetrahedralMesh<ELEMENT_DIM, SPACE_DIM>* AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::mpMesh [protected] |
Mesh to be solved on.
Reimplemented in AbstractNonlinearAssemblerSolverHybrid< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >, LinearParabolicPdeSystemWithCoupledOdeSystemSolver< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >, and AbstractNonlinearAssemblerSolverHybrid< ELEMENT_DIM, SPACE_DIM, 1 >.
Definition at line 83 of file AbstractFeVolumeIntegralAssembler.hpp.
GaussianQuadratureRule<ELEMENT_DIM>* AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::mpQuadRule [protected] |
Quadrature rule for use on normal elements.
Definition at line 86 of file AbstractFeVolumeIntegralAssembler.hpp.
Referenced by AbstractFeVolumeIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM, CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX, INTERPOLATION_LEVEL >::AbstractFeVolumeIntegralAssembler(), and AbstractFeVolumeIntegralAssembler< DIM, DIM, 2, false, true, CARDIAC >::~AbstractFeVolumeIntegralAssembler().
The documentation for this class was generated from the following file:
- pde/src/solver/AbstractFeVolumeIntegralAssembler.hpp