#include <AbstractFeSurfaceIntegralAssembler.hpp>
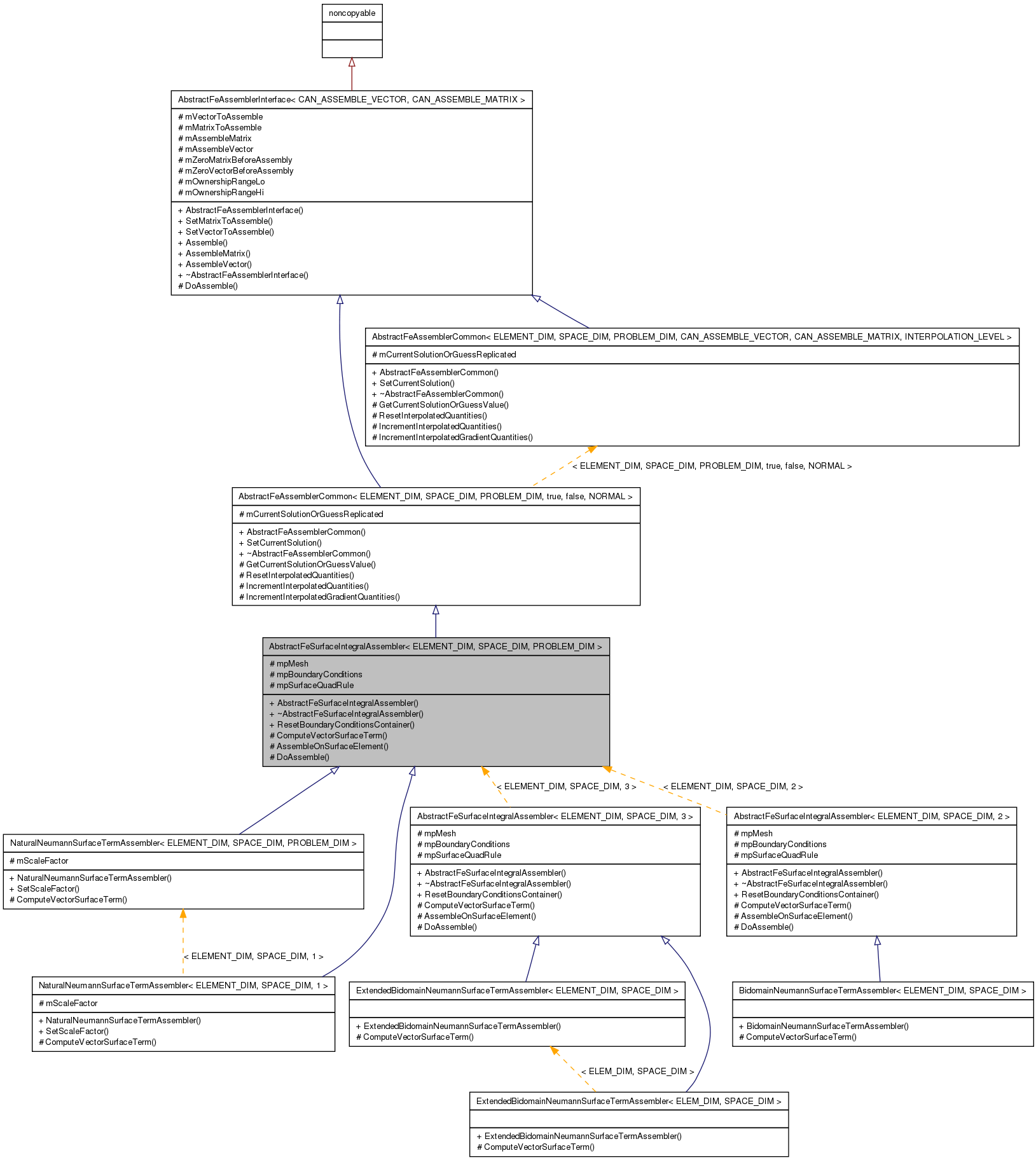
 Inheritance diagram for AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >:
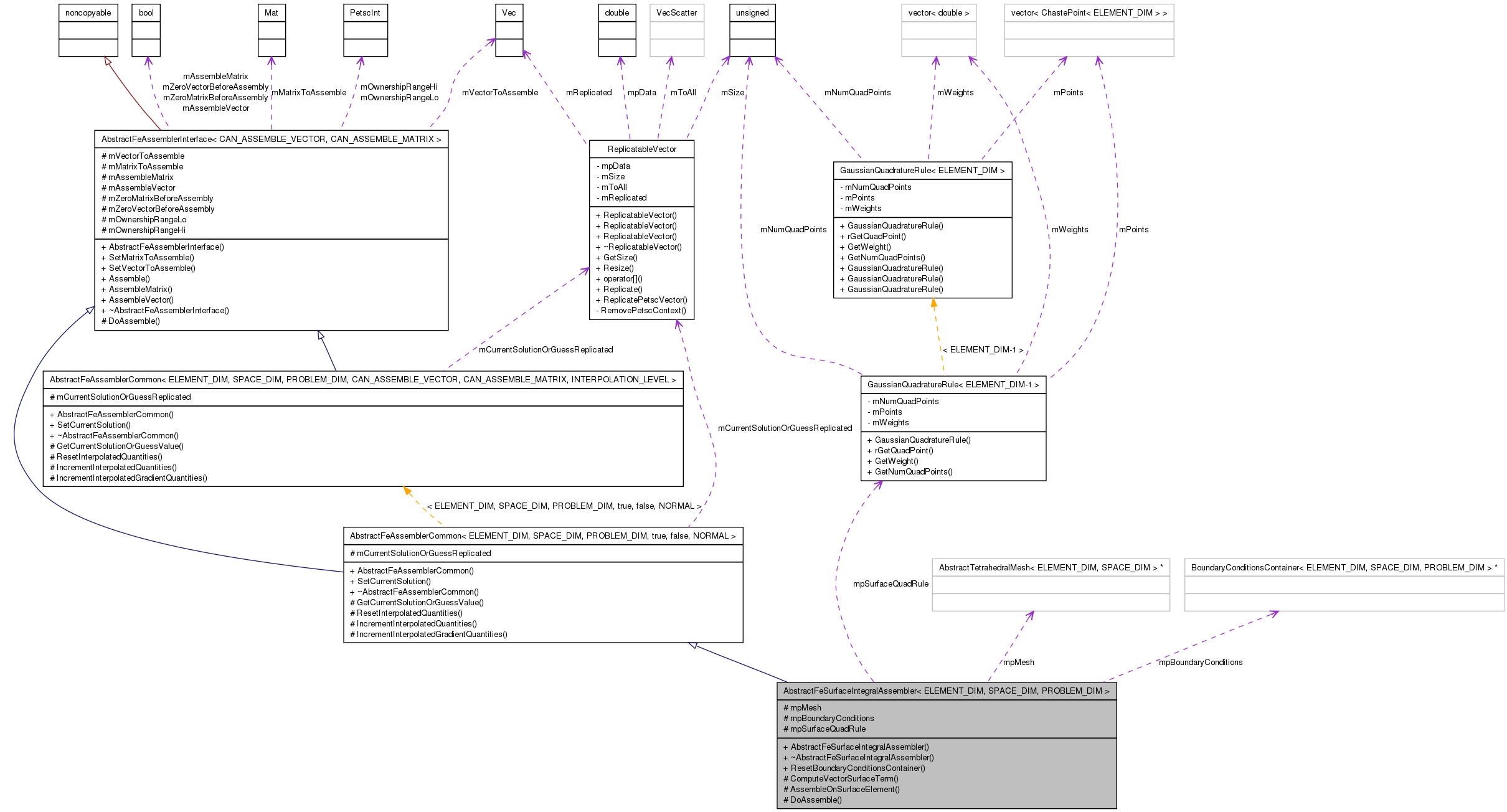
Inheritance diagram for AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >: Collaboration diagram for AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >:
Collaboration diagram for AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >:Public Member Functions | |
| AbstractFeSurfaceIntegralAssembler (AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > *pMesh, BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > *pBoundaryConditions, unsigned numQuadPoints=2) | |
| virtual | ~AbstractFeSurfaceIntegralAssembler () |
| void | ResetBoundaryConditionsContainer (BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > *pBoundaryConditions) |
Protected Types | |
| typedef LinearBasisFunction < ELEMENT_DIM-1 > | SurfaceBasisFunction |
Protected Member Functions | |
| virtual c_vector< double, PROBLEM_DIM *ELEMENT_DIM > | ComputeVectorSurfaceTerm (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, ELEMENT_DIM > &rPhi, ChastePoint< SPACE_DIM > &rX) |
| virtual void | AssembleOnSurfaceElement (const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > &rSurfaceElement, c_vector< double, PROBLEM_DIM *ELEMENT_DIM > &rBSurfElem) |
| void | DoAssemble () |
Protected Attributes | |
| AbstractTetrahedralMesh < ELEMENT_DIM, SPACE_DIM > * | mpMesh |
| BoundaryConditionsContainer < ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > * | mpBoundaryConditions |
| GaussianQuadratureRule < ELEMENT_DIM-1 > * | mpSurfaceQuadRule |
Detailed Description
template<unsigned ELEMENT_DIM, unsigned SPACE_DIM, unsigned PROBLEM_DIM>
class AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >
Similar to AbstractFeVolumeIntegralAssembler but is used for constructing finite element objects that are based on SURFACE INTEGRALS, as opposed to volume integrals.
This class assumes that the concrete class only needs to assemble a vector, not a matrix. (Can be extended in the future if needed).
Hence, the (effectively) pure method, that needs to be implemented, is ComputeVectorSurfaceTerm().
The surface terms is assumed to come from Neumann BCs, so only the surface elements containing non-zero Neumann BCs (from the BoundaryConditionsContainer given) are assembled on.
The interface is the same the volume assemblers.
Definition at line 61 of file AbstractFeSurfaceIntegralAssembler.hpp.
Member Typedef Documentation
typedef LinearBasisFunction<ELEMENT_DIM-1> AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::SurfaceBasisFunction [protected] |
Basis function for use with boundary elements.
Definition at line 74 of file AbstractFeSurfaceIntegralAssembler.hpp.
Constructor & Destructor Documentation
| AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AbstractFeSurfaceIntegralAssembler | ( | AbstractTetrahedralMesh< ELEMENT_DIM, SPACE_DIM > * | pMesh, |
| BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > * | pBoundaryConditions, | ||
| unsigned | numQuadPoints = 2 |
||
| ) |
Constructor
- Parameters:
-
pMesh The mesh pBoundaryConditions The boundary conditions container numQuadPoints Number of quad points (per dimension) to use
Definition at line 149 of file AbstractFeSurfaceIntegralAssembler.hpp.
References AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpSurfaceQuadRule.
| AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::~AbstractFeSurfaceIntegralAssembler | ( | ) | [virtual] |
Destructor
Definition at line 165 of file AbstractFeSurfaceIntegralAssembler.hpp.
Member Function Documentation
| void AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AssembleOnSurfaceElement | ( | const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > & | rSurfaceElement, |
| c_vector< double, PROBLEM_DIM *ELEMENT_DIM > & | rBSurfElem | ||
| ) | [protected, virtual] |
Calculate the contribution of a single surface element with Neumann boundary condition to the linear system.
- Parameters:
-
rSurfaceElement The element to assemble on. rBSurfElem The element's contribution to the RHS vector is returned in this vector of length n, the no. of nodes in this element. There is no need to zero this vector before calling.
- Todo:
- #1321 Improve efficiency of Neumann BC implementation
Definition at line 205 of file AbstractFeSurfaceIntegralAssembler.hpp.
References AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetIndex(), AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetNode(), AbstractElement< ELEMENT_DIM, SPACE_DIM >::GetNumNodes(), and ChastePoint< DIM >::rGetLocation().
| virtual c_vector<double, PROBLEM_DIM*ELEMENT_DIM> AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ComputeVectorSurfaceTerm | ( | const BoundaryElement< ELEMENT_DIM-1, SPACE_DIM > & | rSurfaceElement, |
| c_vector< double, ELEMENT_DIM > & | rPhi, | ||
| ChastePoint< SPACE_DIM > & | rX | ||
| ) | [inline, protected, virtual] |
This method returns the vector to be added to full vector for a given Gauss point in BoundaryElement, ie, essentially the INTEGRAND in the boundary integral part of the definition of the vector. The arguments are the bases, x and current solution computed at the Gauss point.
** This method needs to be overloaded in the concrete class **
- Parameters:
-
rSurfaceElement the element which is being considered. rPhi The basis functions, rPhi(i) = phi_i, i=1..numBases rX The point in space
Reimplemented in BidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM >, ExtendedBidomainNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM >, NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >, ExtendedBidomainNeumannSurfaceTermAssembler< ELEM_DIM, SPACE_DIM >, and NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, 1 >.
Definition at line 89 of file AbstractFeSurfaceIntegralAssembler.hpp.
| void AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::DoAssemble | ( | ) | [protected, virtual] |
Main assemble method. Users should call Assemble() however
Implements AbstractFeAssemblerInterface< CAN_ASSEMBLE_VECTOR, CAN_ASSEMBLE_MATRIX >.
Definition at line 172 of file AbstractFeSurfaceIntegralAssembler.hpp.
References GenericEventHandler< 16, HeartEventHandler >::BeginEvent(), GenericEventHandler< 16, HeartEventHandler >::EndEvent(), BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::EndNeumann(), and AbstractTetrahedralElement< ELEMENT_DIM, SPACE_DIM >::GetStiffnessMatrixGlobalIndices().
| void AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ResetBoundaryConditionsContainer | ( | BoundaryConditionsContainer< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM > * | pBoundaryConditions | ) | [inline] |
Reset the internal boundary conditions container pointer
- Parameters:
-
pBoundaryConditions
Definition at line 140 of file AbstractFeSurfaceIntegralAssembler.hpp.
Member Data Documentation
BoundaryConditionsContainer<ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM>* AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpBoundaryConditions [protected] |
Boundary conditions container
Definition at line 68 of file AbstractFeSurfaceIntegralAssembler.hpp.
Referenced by NaturalNeumannSurfaceTermAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::ComputeVectorSurfaceTerm(), and AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, 2 >::ResetBoundaryConditionsContainer().
AbstractTetrahedralMesh<ELEMENT_DIM, SPACE_DIM>* AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpMesh [protected] |
Mesh to be solved on.
Definition at line 65 of file AbstractFeSurfaceIntegralAssembler.hpp.
GaussianQuadratureRule<ELEMENT_DIM-1>* AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::mpSurfaceQuadRule [protected] |
Quadrature rule for use on boundary elements.
Definition at line 71 of file AbstractFeSurfaceIntegralAssembler.hpp.
Referenced by AbstractFeSurfaceIntegralAssembler< ELEMENT_DIM, SPACE_DIM, PROBLEM_DIM >::AbstractFeSurfaceIntegralAssembler().
The documentation for this class was generated from the following file:
- pde/src/solver/AbstractFeSurfaceIntegralAssembler.hpp