#include <RungeKuttaFehlbergIvpOdeSolver.hpp>

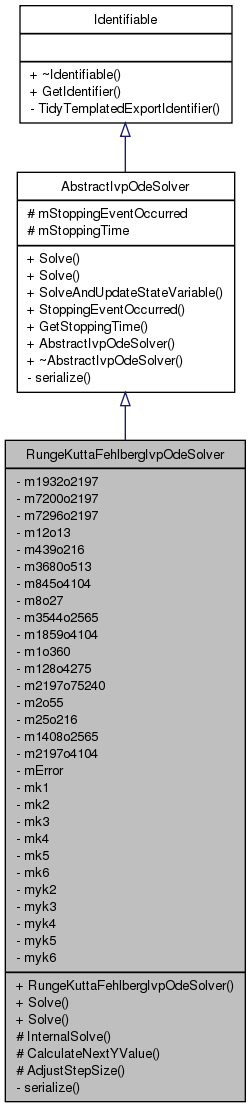
Inheritance diagram for RungeKuttaFehlbergIvpOdeSolver:

Collaboration diagram for RungeKuttaFehlbergIvpOdeSolver:

Public Member Functions
	RungeKuttaFehlbergIvpOdeSolver ()
OdeSolution	Solve (AbstractOdeSystem *pAbstractOdeSystem, std::vector< double > &rYValues, double startTime, double endTime, double timeStep, double ignoredSamplingTime)
void	Solve (AbstractOdeSystem *pAbstractOdeSystem, std::vector< double > &rYValues, double startTime, double endTime, double timeStep)
Protected Member Functions
void	InternalSolve (OdeSolution &rSolution, AbstractOdeSystem *pAbstractOdeSystem, std::vector< double > &rCurrentYValues, std::vector< double > &rWorkingMemory, double startTime, double endTime, double maxTimeStep, double minTimeStep, double tolerance, bool outputSolution)
void	CalculateNextYValue (AbstractOdeSystem *pAbstractOdeSystem, double timeStep, double time, std::vector< double > &rCurrentYValues, std::vector< double > &rNextYValues)
void	AdjustStepSize (double &rCurrentStepSize, const double &rError, const double &rTolerance, const double &rMaxTimeStep, const double &rMinTimeStep)
Private Member Functions
template<class Archive >
void	serialize (Archive &archive, const unsigned int version)
Private Attributes
double	m1932o2197
double	m7200o2197
double	m7296o2197
double	m12o13
double	m439o216
double	m3680o513
double	m845o4104
double	m8o27
double	m3544o2565
double	m1859o4104
double	m1o360
double	m128o4275
double	m2197o75240
double	m2o55
double	m25o216
double	m1408o2565
double	m2197o4104
std::vector< double >	mError
std::vector< double >	mk1
std::vector< double >	mk2
std::vector< double >	mk3
std::vector< double >	mk4
std::vector< double >	mk5
std::vector< double >	mk6
std::vector< double >	myk2
std::vector< double >	myk3
std::vector< double >	myk4
std::vector< double >	myk5
std::vector< double >	myk6
Friends
class	TestRungeKuttaFehlbergIvpOdeSolver
class	boost::serialization::access

Detailed Description

A concrete one step ODE solver class that employs the Runge Kutta Fehlberg adaptive solver (RKF45).

This solver is good for problems where you need to be able to guarantee the accuracy of the answer as it is specified via the tolerance parameter.

The solver should also be reasonably fast as it increases the timestep when the solutions are changing slowly, whilst maintaining accuracy.

Definition at line 56 of file RungeKuttaFehlbergIvpOdeSolver.hpp.

Constructor & Destructor Documentation

RungeKuttaFehlbergIvpOdeSolver::RungeKuttaFehlbergIvpOdeSolver ( )

Constructor.

Definition at line 263 of file RungeKuttaFehlbergIvpOdeSolver.cpp.

Member Function Documentation

void RungeKuttaFehlbergIvpOdeSolver::AdjustStepSize	(	double &	rCurrentStepSize,
		const double &	rError,
		const double &	rTolerance,
		const double &	rMaxTimeStep,
		const double &	rMinTimeStep
	)		`[protected]`

Use the error approximation of the last call to the CalculateNextYValue() method to change the time step appropriately.

Parameters:

rCurrentStepSize	the current step size being used (returns answer via this reference)
rError	the error in the approximation at this time step
rTolerance	the tolerance required
rMaxTimeStep	the maximum timestep to be used
rMinTimeStep	the minimum timestep to be used (to prevent huge loops)

Definition at line 220 of file RungeKuttaFehlbergIvpOdeSolver.cpp.

References EXCEPTION.

Referenced by InternalSolve().

void RungeKuttaFehlbergIvpOdeSolver::CalculateNextYValue	(	AbstractOdeSystem *	pAbstractOdeSystem,
		double	timeStep,
		double	time,
		std::vector< double > &	rCurrentYValues,
		std::vector< double > &	rNextYValues
	)		`[protected]`

Calculate the solution to the ODE system at the next timestep. Updates the mError vector with current error.

Parameters:

pAbstractOdeSystem	the ODE system to solve
timeStep	dt
time	the current time
rCurrentYValues	the current (initial) state
rNextYValues	the state at the next timestep

Definition at line 159 of file RungeKuttaFehlbergIvpOdeSolver.cpp.

References AbstractOdeSystem::EvaluateYDerivatives(), AbstractUntemplatedParameterisedSystem::GetNumberOfStateVariables(), m128o4275, m12o13, m1408o2565, m1859o4104, m1932o2197, m1o360, m2197o4104, m2197o75240, m25o216, m2o55, m3544o2565, m3680o513, m439o216, m7200o2197, m7296o2197, m845o4104, m8o27, mError, mk1, mk2, mk3, mk4, mk5, mk6, myk2, myk3, myk4, myk5, and myk6.

Referenced by InternalSolve().

void RungeKuttaFehlbergIvpOdeSolver::InternalSolve	(	OdeSolution &	rSolution,
		AbstractOdeSystem *	pAbstractOdeSystem,
		std::vector< double > &	rCurrentYValues,
		std::vector< double > &	rWorkingMemory,
		double	startTime,
		double	endTime,
		double	maxTimeStep,
		double	minTimeStep,
		double	tolerance,
		bool	outputSolution
	)		`[protected]`

Method that actually performs the solving on behalf of the public Solve methods.

Parameters:

rSolution	an ODE solution to input data into if requited
pAbstractOdeSystem	the ODE system to solve
rCurrentYValues	the current (initial) state; results will also be returned in here
rWorkingMemory	working memory; same size as rCurrentYValues
startTime	initial time
endTime	time to solve to
maxTimeStep	the maximum size of timestep allowable
minTimeStep	the maximum size of timestep allowable (to prevent huge loops)
tolerance	how accurate the numerical solution must be
outputSolution	whether to output into rSolution (or save time by not doing)

Definition at line 46 of file RungeKuttaFehlbergIvpOdeSolver.cpp.

References AdjustStepSize(), CalculateNextYValue(), AbstractOdeSystem::CalculateStoppingEvent(), AbstractUntemplatedParameterisedSystem::GetNumberOfStateVariables(), mError, mk1, mk2, mk3, mk4, mk5, mk6, AbstractIvpOdeSolver::mStoppingEventOccurred, AbstractIvpOdeSolver::mStoppingTime, myk2, myk3, myk4, myk5, myk6, OdeSolution::rGetSolutions(), OdeSolution::rGetTimes(), and OdeSolution::SetNumberOfTimeSteps().

Referenced by Solve().

template<class Archive >

void RungeKuttaFehlbergIvpOdeSolver::serialize	(	Archive &	archive,
		const unsigned int	version
	)		`[inline, private]`

Archive, never used directly - boost uses this.

Parameters:

archive	the archive
version	the current version of this class

Reimplemented from AbstractIvpOdeSolver.

Definition at line 70 of file RungeKuttaFehlbergIvpOdeSolver.hpp.

OdeSolution RungeKuttaFehlbergIvpOdeSolver::Solve	(	AbstractOdeSystem *	pAbstractOdeSystem,
		std::vector< double > &	rYValues,
		double	startTime,
		double	endTime,
		double	timeStep,
		double	ignoredSamplingTime
	)		`[virtual]`

Solves a system of ODEs using a specified one-step ODE solver and returns the solution as an OdeSolution object.

Parameters:

pAbstractOdeSystem	pointer to the concrete ODE system to be solved
rYValues	a standard vector specifying the intial condition of each solution variable in the system (this can be the initial conditions vector stored in the ODE system)
startTime	the time at which the initial conditions are specified
endTime	the time to which the system should be solved and the solution returned
timeStep	the time interval to be used by the solver
ignoredSamplingTime	the interval at which to sample the solution to the ODE system (ignored in this class as the timestep is variable)

Returns:: OdeSolution is an object containing an integer of the number of equations, a stdAbstractOdeSystem::vector of times and a std::vector of std::vectors where each of those vectors contains the solution for one variable of the ODE system at those times.

Implements AbstractIvpOdeSolver.

Definition at line 284 of file RungeKuttaFehlbergIvpOdeSolver.cpp.

References AbstractOdeSystem::CalculateStoppingEvent(), EXCEPTION, AbstractUntemplatedParameterisedSystem::GetNumberOfStateVariables(), InternalSolve(), and AbstractIvpOdeSolver::mStoppingEventOccurred.

void RungeKuttaFehlbergIvpOdeSolver::Solve	(	AbstractOdeSystem *	pAbstractOdeSystem,
		std::vector< double > &	rYValues,
		double	startTime,
		double	endTime,
		double	timeStep
	)		`[virtual]`

Second version of Solve. Solves a system of ODEs using a specified one-step ODE solver. This method does not return the solution and therefore does not take in a sampling time. Instead, the mStateVariables component in the ODE system object is updated.

Parameters:

pAbstractOdeSystem	pointer to the concrete ODE system to be solved
rYValues	a standard vector specifying the intial condition of each solution variable in the system (this can be the initial conditions vector stored in the ODE system)
startTime	the time at which the initial conditions are specified
endTime	the time to which the system should be solved and the solution returned
timeStep	the time interval to be used by the solver