#include <SchmidCostaExponentialLaw2d.hpp>
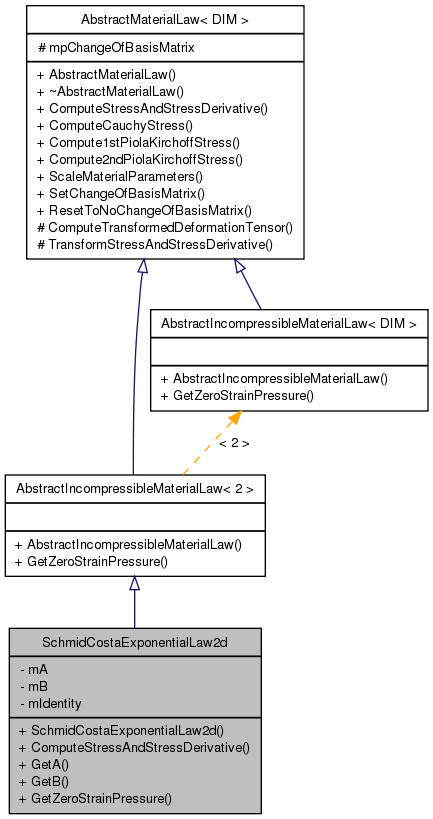
 Inheritance diagram for SchmidCostaExponentialLaw2d:
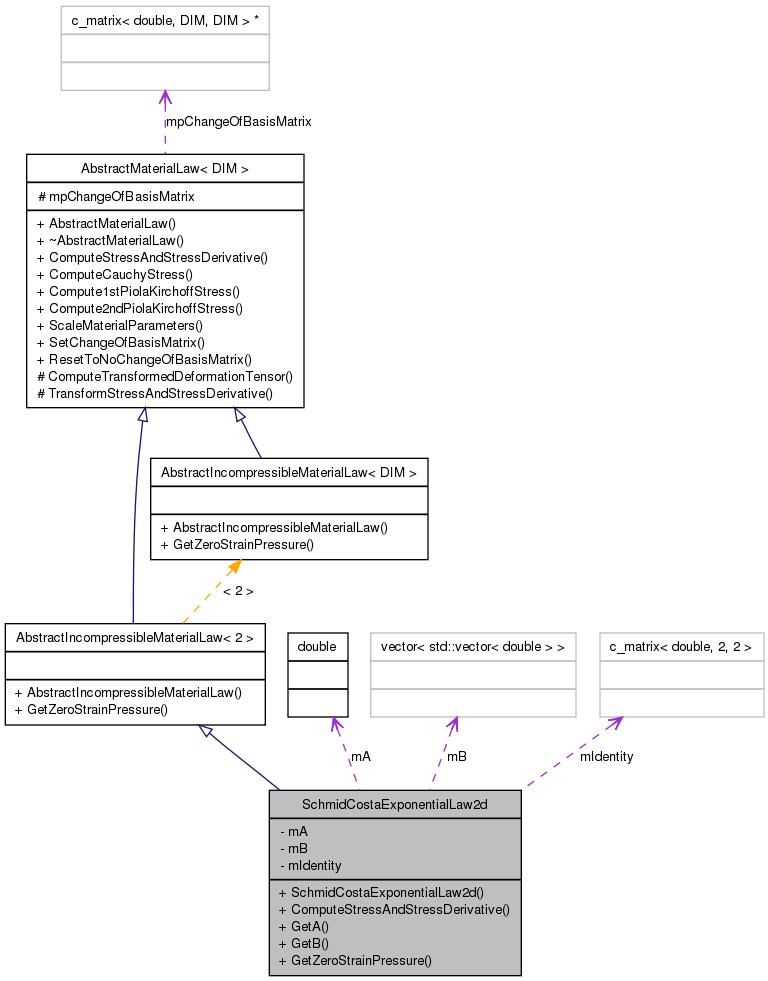
Inheritance diagram for SchmidCostaExponentialLaw2d: Collaboration diagram for SchmidCostaExponentialLaw2d:
Collaboration diagram for SchmidCostaExponentialLaw2d:Public Member Functions | |
| SchmidCostaExponentialLaw2d () | |
| void | ComputeStressAndStressDerivative (c_matrix< double, 2, 2 > &rC, c_matrix< double, 2, 2 > &rInvC, double pressure, c_matrix< double, 2, 2 > &rT, FourthOrderTensor< 2, 2, 2, 2 > &rDTdE, bool computeDTdE) |
| double | GetA () |
| std::vector< std::vector < double > > | GetB () |
| double | GetZeroStrainPressure () |
Private Attributes | |
| double | mA |
| std::vector< std::vector < double > > | mB |
| c_matrix< double, 2, 2 > | mIdentity |
Detailed Description
A 2d version of the material law in Costa, Holmes, McCulloch "Modelling Cardiac Mechanical Properties in Three Dimensions" Philo. Trans. R. Soc.
W = a[exp(Q)-1]/2 where Q = bff*Eff^2 + bfs*Efs^2 + bsf*Esf^2 + bss*Ess^2
where the parameters are taken from the fitting in Schmid,Nash,Young,Hunter "Myocardial Material Parameter Estimation - A Comparative Study for Simple Shear" Transactions of the ASME.
Note, by default, the fibre direction is assumed to be THE X-DIRECTION, and the sheet direction the Y-DIRECTION (ie sheets in the XY plane). Call SetChangeOfBasisMatrix() before ComputeStressAndStressDerivative(), with the matrix P = [fibre_vec, sheet_vec, normal_vec] if this is not the case.
Definition at line 58 of file SchmidCostaExponentialLaw2d.hpp.
Constructor & Destructor Documentation
| SchmidCostaExponentialLaw2d::SchmidCostaExponentialLaw2d | ( | ) |
Constructor.
Definition at line 38 of file SchmidCostaExponentialLaw2d.cpp.
Member Function Documentation
| void SchmidCostaExponentialLaw2d::ComputeStressAndStressDerivative | ( | c_matrix< double, 2, 2 > & | rC, |
| c_matrix< double, 2, 2 > & | rInvC, | ||
| double | pressure, | ||
| c_matrix< double, 2, 2 > & | rT, | ||
| FourthOrderTensor< 2, 2, 2, 2 > & | rDTdE, | ||
| bool | computeDTdE | ||
| ) |
Compute the (2nd Piola Kirchoff) stress T and the stress derivative dT/dE for a given strain.
NOTE: the strain E is not expected to be passed in, instead the Lagrangian deformation tensor C is required (recall, E = 0.5(C-I))
dT/dE is a fourth-order tensor, where dT/dE[M][N][P][Q] = dT^{MN}/dE_{PQ}
- Parameters:
-
rC The Lagrangian deformation tensor (F^T F) rInvC The inverse of C. Should be computed by the user. (Change this?) pressure the current pressure rT the stress will be returned in this parameter rDTdE the stress derivative will be returned in this parameter, assuming the final parameter is true computeDTdE a boolean flag saying whether the stress derivative is required or not.
Definition at line 66 of file SchmidCostaExponentialLaw2d.cpp.
References AbstractMaterialLaw< DIM >::ComputeTransformedDeformationTensor(), mA, mB, mIdentity, AbstractMaterialLaw< DIM >::TransformStressAndStressDerivative(), and FourthOrderTensor< DIM1, DIM2, DIM3, DIM4 >::Zero().
| double SchmidCostaExponentialLaw2d::GetA | ( | ) |
| std::vector< std::vector< double > > SchmidCostaExponentialLaw2d::GetB | ( | ) |
| double SchmidCostaExponentialLaw2d::GetZeroStrainPressure | ( | ) | [virtual] |
Get the pressure corresponding to E=0, ie C=identity.
Implements AbstractIncompressibleMaterialLaw< 2 >.
Definition at line 135 of file SchmidCostaExponentialLaw2d.cpp.
Member Data Documentation
double SchmidCostaExponentialLaw2d::mA [private] |
Parameter a. (kPa)
Definition at line 63 of file SchmidCostaExponentialLaw2d.hpp.
Referenced by ComputeStressAndStressDerivative(), GetA(), and SchmidCostaExponentialLaw2d().
std::vector<std::vector<double> > SchmidCostaExponentialLaw2d::mB [private] |
Matrix of parameters b (dimensionless).
Definition at line 66 of file SchmidCostaExponentialLaw2d.hpp.
Referenced by ComputeStressAndStressDerivative(), GetB(), and SchmidCostaExponentialLaw2d().
c_matrix<double,2,2> SchmidCostaExponentialLaw2d::mIdentity [private] |
2D identity matrix.
Definition at line 69 of file SchmidCostaExponentialLaw2d.hpp.
Referenced by ComputeStressAndStressDerivative(), and SchmidCostaExponentialLaw2d().
The documentation for this class was generated from the following files:
- continuum_mechanics/src/problem/material_laws/SchmidCostaExponentialLaw2d.hpp
- continuum_mechanics/src/problem/material_laws/SchmidCostaExponentialLaw2d.cpp