#include <AbstractMaterialLaw.hpp>
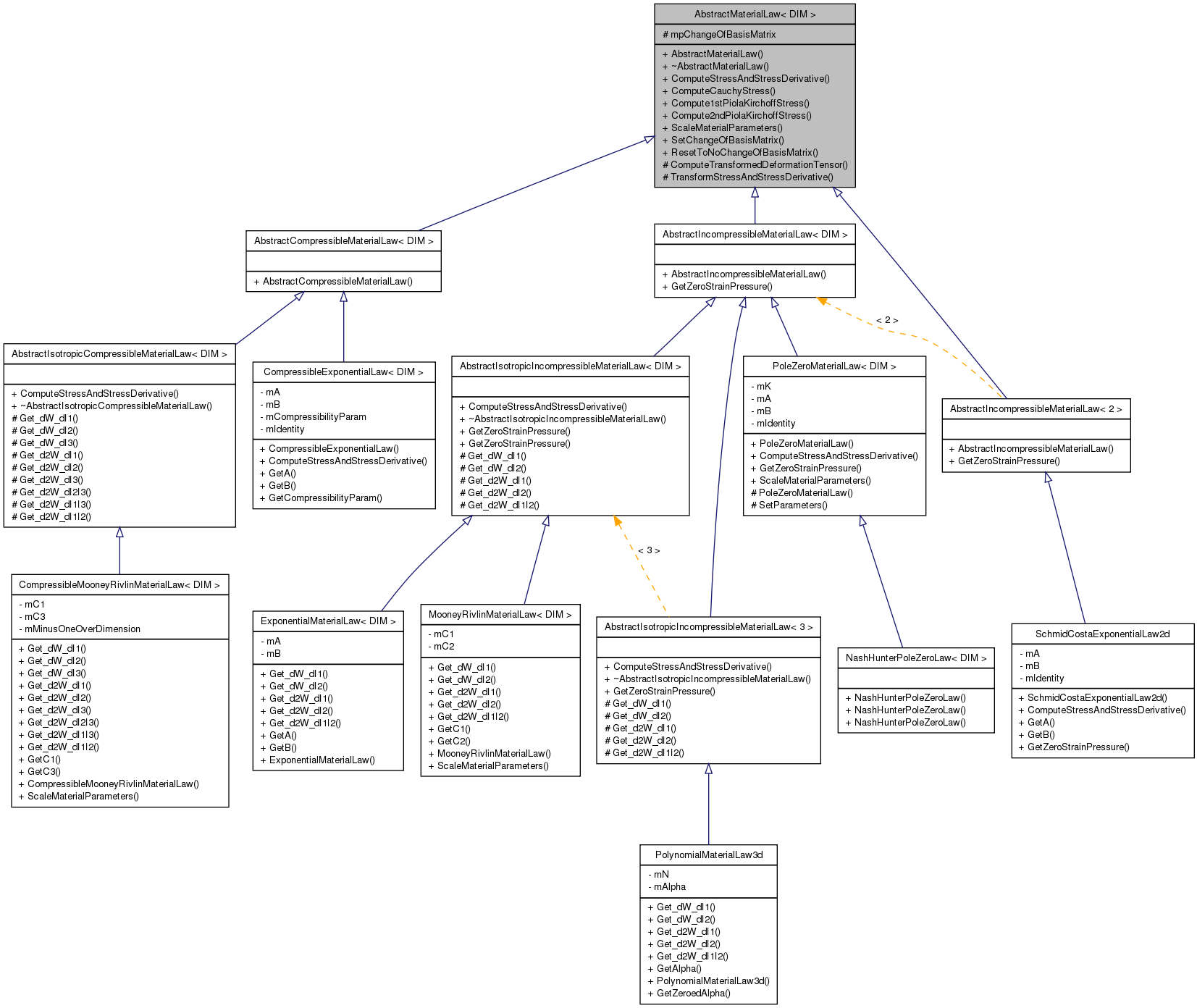
 Inheritance diagram for AbstractMaterialLaw< DIM >:
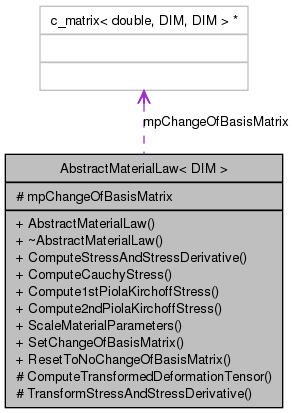
Inheritance diagram for AbstractMaterialLaw< DIM >: Collaboration diagram for AbstractMaterialLaw< DIM >:
Collaboration diagram for AbstractMaterialLaw< DIM >:Public Member Functions | |
| AbstractMaterialLaw () | |
| virtual | ~AbstractMaterialLaw () |
| virtual void | ComputeStressAndStressDerivative (c_matrix< double, DIM, DIM > &rC, c_matrix< double, DIM, DIM > &rInvC, double pressure, c_matrix< double, DIM, DIM > &rT, FourthOrderTensor< DIM, DIM, DIM, DIM > &rDTdE, bool computeDTdE)=0 |
| void | ComputeCauchyStress (c_matrix< double, DIM, DIM > &rF, double pressure, c_matrix< double, DIM, DIM > &rSigma) |
| void | Compute1stPiolaKirchoffStress (c_matrix< double, DIM, DIM > &rF, double pressure, c_matrix< double, DIM, DIM > &rS) |
| void | Compute2ndPiolaKirchoffStress (c_matrix< double, DIM, DIM > &rC, double pressure, c_matrix< double, DIM, DIM > &rT) |
| virtual void | ScaleMaterialParameters (double scaleFactor) |
| void | SetChangeOfBasisMatrix (c_matrix< double, DIM, DIM > &rChangeOfBasisMatrix) |
| void | ResetToNoChangeOfBasisMatrix () |
Protected Member Functions | |
| void | ComputeTransformedDeformationTensor (c_matrix< double, DIM, DIM > &rC, c_matrix< double, DIM, DIM > &rInvC, c_matrix< double, DIM, DIM > &rCTransformed, c_matrix< double, DIM, DIM > &rInvCTransformed) |
| void | TransformStressAndStressDerivative (c_matrix< double, DIM, DIM > &rT, FourthOrderTensor< DIM, DIM, DIM, DIM > &rDTdE, bool transformDTdE) |
Protected Attributes | |
| c_matrix< double, DIM, DIM > * | mpChangeOfBasisMatrix |
Detailed Description
template<unsigned DIM>
class AbstractMaterialLaw< DIM >
A hyper-elastic material law for finite elasticity
The law is given by a strain energy function W(E), where E is the strain, such that the (2nd Piola-Kirchhoff) stress T = dW/dE
Definition at line 55 of file AbstractMaterialLaw.hpp.
Constructor & Destructor Documentation
| AbstractMaterialLaw< DIM >::AbstractMaterialLaw | ( | ) |
Constuctor
Definition at line 39 of file AbstractMaterialLaw.cpp.
| virtual AbstractMaterialLaw< DIM >::~AbstractMaterialLaw | ( | ) | [inline, virtual] |
Destructor
Definition at line 95 of file AbstractMaterialLaw.hpp.
Member Function Documentation
| void AbstractMaterialLaw< DIM >::Compute1stPiolaKirchoffStress | ( | c_matrix< double, DIM, DIM > & | rF, |
| double | pressure, | ||
| c_matrix< double, DIM, DIM > & | rS | ||
| ) |
Compute the 1st Piola Kirchoff stress, given the deformation gradient F and the pressure. The 1st Piola Kirchoff stress given by
S^{Mi} = T^{MN} F^i_M,
where T is the 2nd PK stress, dW/dE.
Note that this stress is not symmetric and the least useful of the three stresses.
- Parameters:
-
rF the deformation gradient pressure the pressure rS an empty matrix, which will be filled in with the stress
Note: the compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0
Definition at line 83 of file AbstractMaterialLaw.cpp.
References Inverse().
| void AbstractMaterialLaw< DIM >::Compute2ndPiolaKirchoffStress | ( | c_matrix< double, DIM, DIM > & | rC, |
| double | pressure, | ||
| c_matrix< double, DIM, DIM > & | rT | ||
| ) |
Compute the 2nd Piola Kirchoff stress, given the deformation tensor C and the pressure. The 2nd Piola Kirchoff stress given by
T^{MN} = dW/dE_{MN} = 2dW/dC_{MN}
- Parameters:
-
rC the Lagrange deformation tensor (C=F^T F), *not* F, and *not* E pressure the pressure rT an empty matrix, which will be filled in with the stress
Note: to compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0
Definition at line 100 of file AbstractMaterialLaw.cpp.
References Inverse().
| void AbstractMaterialLaw< DIM >::ComputeCauchyStress | ( | c_matrix< double, DIM, DIM > & | rF, |
| double | pressure, | ||
| c_matrix< double, DIM, DIM > & | rSigma | ||
| ) |
Compute the Cauchy stress (the true stress), given the deformation gradient F and the pressure. The Cauchy stress is given by
sigma^{ij} = (1/detF) F^i_M T^{MN} F^j_N
where T is the 2nd Piola Kirchoff stress, dW/dE
- Parameters:
-
rF the deformation gradient pressure the pressure rSigma an empty matrix, which will be filled in with the Cauchy stress
Note: the compute the material part of the stress (the pressure-independent part), just pass in pressure=0.0
Definition at line 45 of file AbstractMaterialLaw.cpp.
References Determinant(), and Inverse().
| virtual void AbstractMaterialLaw< DIM >::ComputeStressAndStressDerivative | ( | c_matrix< double, DIM, DIM > & | rC, |
| c_matrix< double, DIM, DIM > & | rInvC, | ||
| double | pressure, | ||
| c_matrix< double, DIM, DIM > & | rT, | ||
| FourthOrderTensor< DIM, DIM, DIM, DIM > & | rDTdE, | ||
| bool | computeDTdE | ||
| ) | [pure virtual] |
Compute the (2nd Piola Kirchoff) stress T and the stress derivative dT/dE for a given strain.
NOTE: the strain E is not expected to be passed in, instead the Lagrangian deformation tensor C is required (recall, E = 0.5(C-I))
dTdE is a fourth-order tensor, where dTdE(M,N,P,Q) = dT^{MN}/dE_{PQ}
- Parameters:
-
rC The Lagrangian deformation tensor (F^T F) rInvC The inverse of C. Should be computed by the user. pressure the current pressure rT the stress will be returned in this parameter rDTdE the stress derivative will be returned in this parameter, assuming the final parameter is true computeDTdE a boolean flag saying whether the stress derivative is required or not.
Implemented in AbstractIsotropicCompressibleMaterialLaw< DIM >, AbstractIsotropicIncompressibleMaterialLaw< DIM >, CompressibleExponentialLaw< DIM >, PoleZeroMaterialLaw< DIM >, and AbstractIsotropicIncompressibleMaterialLaw< 3 >.
Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), and CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement().
| void AbstractMaterialLaw< DIM >::ComputeTransformedDeformationTensor | ( | c_matrix< double, DIM, DIM > & | rC, |
| c_matrix< double, DIM, DIM > & | rInvC, | ||
| c_matrix< double, DIM, DIM > & | rCTransformed, | ||
| c_matrix< double, DIM, DIM > & | rInvCTransformed | ||
| ) | [protected] |
Transform the input (C and inv(C), where C in the deformation tensor) to the local coordinate system
- Parameters:
-
rC deformation tensor C (input) rInvC inverse of C (input) rCTransformed P^T C P (output) rInvCTransformed P^T inv(C) P (output)
Definition at line 132 of file AbstractMaterialLaw.cpp.
Referenced by SchmidCostaExponentialLaw2d::ComputeStressAndStressDerivative().
| void AbstractMaterialLaw< DIM >::ResetToNoChangeOfBasisMatrix | ( | ) |
Reset back to no change of basis matrix
Definition at line 126 of file AbstractMaterialLaw.cpp.
| void AbstractMaterialLaw< DIM >::ScaleMaterialParameters | ( | double | scaleFactor | ) | [virtual] |
Set a scale factor by which (dimensional) material parameters are scaled. This method can be optionally implemented in the child class; if no implementation is made an exception is thrown. A scale factor may be used/needed to improve GMRES convergence. Note that is a material law is scaled like this any dimensionally equivalent terms (eg gravity, tractions, active tensions) must also be scaled. Also, computed pressure will come out scaled.
- Parameters:
-
scaleFactor the scale factor
Reimplemented in CompressibleMooneyRivlinMaterialLaw< DIM >, MooneyRivlinMaterialLaw< DIM >, and PoleZeroMaterialLaw< DIM >.
Definition at line 112 of file AbstractMaterialLaw.cpp.
References EXCEPTION.
| void AbstractMaterialLaw< DIM >::SetChangeOfBasisMatrix | ( | c_matrix< double, DIM, DIM > & | rChangeOfBasisMatrix | ) |
Some material laws (eg pole-zero) may have preferred directions (eg fibre direction), but be implemented to assume the preferred directions are parallel to the X-axis etc. Call this with the change of basis matrix and C will be transformed from the Lagrangian coordinate system to the appropriate coordinate system before used to calculate T, which will then be transformed from the appropriate coordinate system back to the Lagrangian coordinate system before being returned, as will dTdE
Note that no copy of this matrix is taken, so the original matrix must persist whilst this class is used. Call ResetToNoChangeOfBasisMatrix() if necessary.
The change of matrix should have the form (writing the preferred directions as fibre, sheet and normal, as in heart simulations): P = [a_f a_s a_n], where each a_i is a vector.
- Parameters:
-
rChangeOfBasisMatrix Change of basis matrix.
Definition at line 120 of file AbstractMaterialLaw.cpp.
Referenced by IncompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement(), and CompressibleNonlinearElasticitySolver< DIM >::AssembleOnElement().
| void AbstractMaterialLaw< DIM >::TransformStressAndStressDerivative | ( | c_matrix< double, DIM, DIM > & | rT, |
| FourthOrderTensor< DIM, DIM, DIM, DIM > & | rDTdE, | ||
| bool | transformDTdE | ||
| ) | [protected] |
Transform the output (T and dTdE) back to the original coordinate system
- Parameters:
-
rT stress being computed rDTdE the stress derivative to be transformed (assuming the final parameter is true) transformDTdE a boolean flag saying whether the stress derivative is to be transformed or not
Definition at line 153 of file AbstractMaterialLaw.cpp.
Referenced by SchmidCostaExponentialLaw2d::ComputeStressAndStressDerivative().
Member Data Documentation
c_matrix<double,DIM,DIM>* AbstractMaterialLaw< DIM >::mpChangeOfBasisMatrix [protected] |
Some material laws are based on a particular local set of preferred directions, eg anisotropic cardiac laws, which use the fibre sheet and normal directions. This matrix can defines the orientation and should set before T and dTdE are computed.
The change of matrix should have the form P = [a_f a_s a_n], where each a_i is a vector.
Definition at line 65 of file AbstractMaterialLaw.hpp.
The documentation for this class was generated from the following files:
- continuum_mechanics/src/problem/material_laws/AbstractMaterialLaw.hpp
- continuum_mechanics/src/problem/material_laws/AbstractMaterialLaw.cpp